مدلسازی شبکه و ارزیابی سیستمهای پیچیده
تعداد بازدید: 2879
زمان مطالعه: 16 دقیقه
فهرست مطالب این نوشته
مفاهیم مدلسازی و ارزیابی (Modelling and evaluation concepts)
روش‌های توضیح داده شده در پست قبلی برای سیستم ها و شبکه‌هایی که دارای ساختار سری و موازی هستند دارای کاربردی محدود است. بسیاری از سیستم‌ها یا این نوع ساختار ساده را ندارند و یا منطق عملیاتی پیچیده‌ای دارند. مدلسازی و روش‌های ارزیابی اضافی به منظور تعیین قابلیت اطمینان چنین سیستم‌هایی ضروری است. یک سیستم معمولی که ساختار سری/موازی ندارد، شبکه‌ای از نوع پل است که در شکل (1) نشان داده شده است. این سیستم اغلب برای نشان دادن روش‌ها در سیستمهای پیچیده استفاده میشود و می‌تواند در بسیاری از کاربردهای مهندسی مورد استفاده قرار گیرد.
در اینجا به تعریف‌هایی از شبکه وابستگی عضوها به صورت متوالی و موازی در تشکیل سیستم می‌پردازیم:
الف: سیستمهای با شبکه متوالی: از دیدگاه قابلیت اطمینان برای عملکرد صحیح یک سیستم با شبکه متوالی باید همه عضوهای آن در حال کار باشد و بنابراین از کار افتادن هر یک از عضوها موجب از کار افتادن سیستم میشود.
ب: سیستمهای با شبکه موازی: از دیدگاه قابلیت اطمینان هرگاه فقط یکی از عضوهای سیستمی با شبکه موازی سالم باشد سیستم همچنان دارای عملکرد انتظاری خواهد بود و بنابراین فقط زمانی که کلیه عضوها از کار بیفتد موجب از کار افتادن سیستم میشود.
این تعریف‌ها زمینه‌ای برای ارتباط با بحث توزیع دوجمله‌ای فراهم می‌آورد. یک سیستم متوالی عبارت از سیستمی بدون عضو مازاد و یک سیستم موازی عبارت از سیستمی با کلیه عضوهای مازاد می‌باشد.
شبکه وابستگی متوالی و موازی از متداول‌ترین و ساده‌ترین ارتباط‌های میان عضوها در تشکیل یک سیستم با سطوح مختلفی از پیچیدگی است و برای تحلیل آن‌ها نیاز به شیوه‌های ویژه‌ای می‌باشد. نمایش شبکه قابلیت اطمینان با استفاده از نمودار جعبه‌ای صورت می‌گیرد.
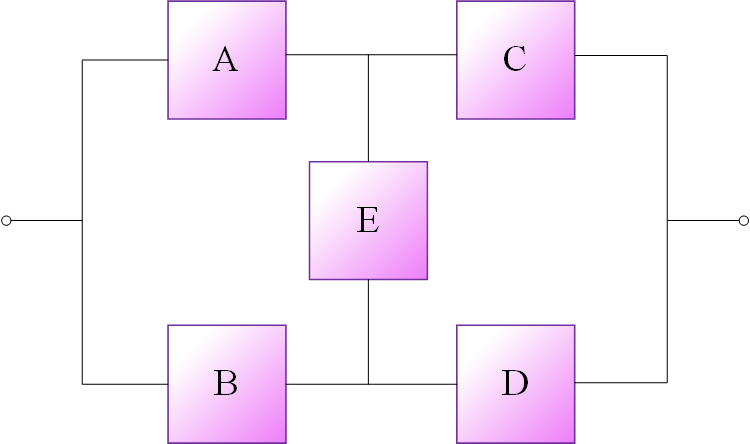
در بررسی عینی شکل (1) ملاحظه میشود که وابستگی میان عضوها، وابستگی متوالی و یا موازی نیست. برای تحلیل این نوع سیستم‌ها تعدادی شیوه‌های حل به شرح در پی آمده در اختیار است:
1- روش احتمال شرطی (Conditional Probability Approach)
2- تحلیل مجموعه انقطاع و اتصال (Cut & Tie Set Analysis)
3- استفاده از نمودارهای درخت (Tree Diagrams)
4- استفاده از نمودارهای منطقی (Logic Diagrams)
5- شیوه آرایه اتصال (Connection Matrix Technique)
مفاهیم مدلسازی و ارزیابی (Modelling and evaluation concepts)
در بررسی عینی شکل (1) ملاحظه میشود که وابستگی میان عضوها، وابستگی متوالی و یا موازی نیست. برای تحلیل این نوع سیستم‌ها تعدادی شیوه‌های حل به شرح در پی آمده در اختیار است:
1- روش احتمال شرطی (Conditional Probability Approach)
2- تحلیل مجموعه انقطاع و اتصال (Cut & Tie Set Analysis)
3- استفاده از نمودارهای درخت (Tree Diagrams)
4- استفاده از نمودارهای منطقی (Logic Diagrams)
5- شیوه آرایه اتصال (Connection Matrix Technique)
رابطه (1)
$$\begin{array}{l}
P(sys\;.\;S/F) = P(sys\;.\;S/F|{X_G})P({X_G})\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + P(sys\;.\;S/F|{X_B})P({X_B})
\end{array}$$
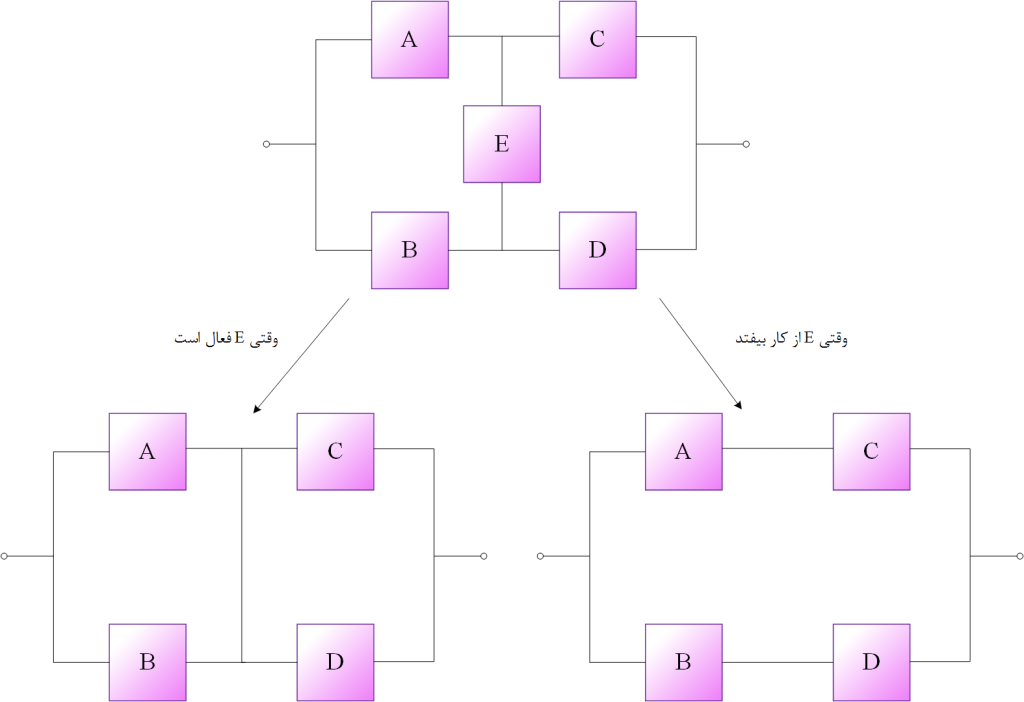
مثال (1): با در نظر گرفتن شکل (2) ملاحظه میشود که عملکرد صحیح سیستم مستلزم عملکرد صحیح عضوها در حداقل یکی از مسیرهای $AC$، $BD$ و $AED$ و یا $BEC$ است. مطلوب است ارزیابی پارامتری و همچنین تعیین مقدار قابلیت اطمینان سیستم برحسب قابلیت اطمینان عضوهای آن مشروط بر آن که قابلیت اطمینان هر یک از عضوها برابر 0.99 باشد.
در بررسی عینی شکل (1) ملاحظه میشود که وابستگی میان عضوها، وابستگی متوالی و یا موازی نیست. برای تحلیل این نوع سیستم‌ها تعدادی شیوه‌های حل به شرح در پی آمده در اختیار است:
1- روش احتمال شرطی (Conditional Probability Approach)
2- تحلیل مجموعه انقطاع و اتصال (Cut & Tie Set Analysis)
3- استفاده از نمودارهای درخت (Tree Diagrams)
4- استفاده از نمودارهای منطقی (Logic Diagrams)
5- شیوه آرایه اتصال (Connection Matrix Technique)
الف- با شرط سالم بودن و عملکرد عضو
$${R_s}(if\;{E_G}) = (1 – {Q_A}{Q_B})(1 – {Q_C}{Q_D})$$
ب- با شرط از کار افتادن عضو
$${R_s}(if\;\;{E_B}) = 1 – (1 – {R_A}{R_C})(1 – {R_B}{R_D})$$
رابطه (2)
$$\begin{array}{l}
{R_s} = (1 - {Q_A}{Q_B})(1 - {Q_C}{Q_D}){R_E}\\
\,\,\,\,\,\,\,\,\, + (1 - (1 - {R_A}{R_C})(1 - {R_B}{R_D})){Q_E}\\
\,\,\,\,\,\,\,\,\, = {R_A}{R_C} + {R_B}{R_D} + {R_A}{R_D}{R_E}\\
\,\,\,\,\,\,\,\,\, + {R_B}{R_C}{R_E} - {R_A}{R_B}{R_C}{R_D}\\
\;\;\;\;\;\; - {R_A}{R_C}{R_D}{R_E} - {R_A}{R_B}{R_C}{R_E}\\
\;\;\;\;\;\; - {R_B}{R_C}{R_D}{R_E} - {R_A}{R_B}{R_D}{R_E}\\
\;\;\;\;\;\; + 2{R_A}{R_B}{R_C}{R_D}{R_E}
\end{array}$$
هرگاه:
$${R_A} = {R_B} = {R_C} = {R_D} = {R_E} = R$$
$${R_s} = 2{R^2} + 2{R^3} – 5{R^4} + 2{R^5}$$
هرگاه $R = 0.99$ باشد خواهیم داشت:
$${R_s} = 0.99979805$$
روش مجموعه انقطاع (Cut Set Method)
مفاهیم مجموعه انقطاع
این روش بنا به دو دلیل عمده، یکی از مؤثرترین روش‌ها در ارزیابی قابلیت اطمینان سیستم‌ها شناخته شده است:
1- کاربردپذیری در برنامه‌نویسی رایانه‌ای جهت تحلیل مؤثر و سریع هرگونه شبکه برای سیستم‌ها
2- امکان‌پذیری شناسایی مستقیم طرق مختلف از کار افتادن سیستم
طبق تعریف مجموعه انقطاع عبارت از مجموعه‌ای از عضوهای سیستم است که شکست آن‌ها موجب شکست سیستم میشود. به بیانی بر مبنای نمودار شبکه قابلیت اطمینان، مجموعه کمترین عضوهایی که شکست آن‌ها موجب انقطاع همه مسیرها از ورودی به خروجی میشود مورد شناسایی واقع میشود و بنابراین سیستم با عملکرد حداقل یکی از این عضوها، از کار نخواهد افتاد.
با تحلیل نمودار شکل (1) با روش مجموعه انقطاع جدول (1) به دست می‌آید.
| شماره کوچکترین مجموعه انقطاع | عضوهای هر مجموعه انقطاع |
|---|---|
| 1 | AB |
| 2 | CD |
| 3 | AED |
| 4 | BEC |
روش استفاده از مجموعه‌های انقطاع (Application of Cut Sets)
به منظور ارزیابی قابلیت اطمینان (یا نااطمینانی) سیستم، مجموعه‌های کمترین عضوهایی که حالت‌های شکست سیستم را به وجود می‌آورند باید در الحاق با یکدیگر در نظر گرفته شود. طبق تعریف بدیهی است که همه عضوهای هر مجموعه انقطاع باید از کار بیفتد تا موجب شکست سیستم شود. بنابراین می‌توان اصول شبکه موازی را برای آن‌ها به کار برد. همچنین با توجه به این که هر یک از مجموعه‌های انقطاع موجب وقوع شکست سیستم میشود، اصول شبکه متوالی برای مجموعه‌های انقطاع در عملکرد سیستم حاکم خواهد بود. با تلفیق این اصول و بر مبنای جدول (1) نموداری مطابق شکل (3) حاصل میشود.
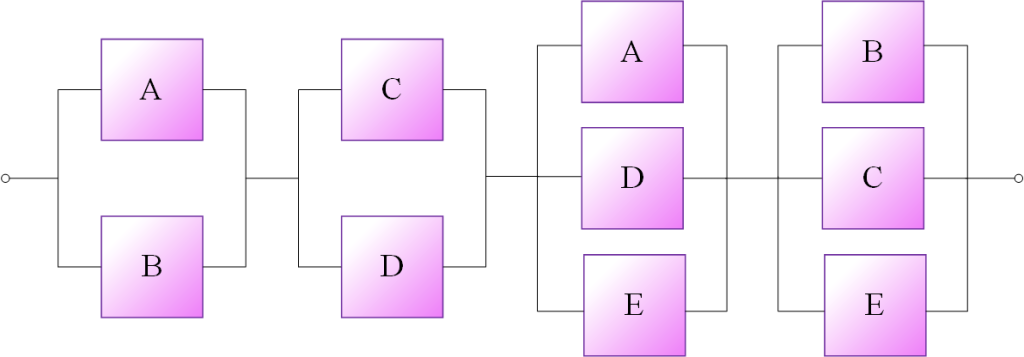
اگرچه این مجموعه‌های انقطاع شبکه‌ای متوالی تشکیل می‌دهد ولی مفاهیم و روش‌های محاسباتی شبکه متوالی برای آن مستقیماً کاربردپذیر نیست زیرا یک عضو معین در دو مجموعه انقطاع و یا بیشتر تکرار میشود. به عنوان مثال عضو در مجموعه انقطاع و در شکل (3) تکرار شده است.
در هر صورت مفهوم اجتماع برای مجموعه‌های شکست حاکم است و با نشان دادن احتمال وقوع هر مجموعه انقطاع در تعیین احتمال شکست سیستم خواهیم داشت:
رابطه (3)
$${Q_s} = P({C_1} \cup {C_2} \cup {C_3} \cup ... \cup {C_i} \cup ... \cup {C_n})$$
مثال (2): مطلوب است کاربرد روش مجموعه انقطاع برای تحلیل مثال (1).
$$\begin{array}{l}
{Q_s} = P({C_1} \cup {C_2} \cup {C_3} \cup {C_4})\\
\;\;\;\; = P({C_1}) + P({C_2}) + P({C_3}) + P({C_4}) – P({C_1} \cap {C_2})\\
\;\;\;\;\;\; – P({C_1} \cap {C_3}) – P({C_1} \cap {C_4}) – P({C_2} \cap {C_3})\\
\;\;\;\;\;\; – P({C_2} \cap {C_4}) – P({C_3} \cap {C_4}) + P({C_1} \cap {C_2} \cap {C_3})\\
\;\;\;\;\;\; + P({C_1} \cap {C_2} \cap {C_4}) + P({C_1} \cap {C_3} \cap {C_4})\\
\;\;\;\;\;\; + P({C_2} \cap {C_3} \cap {C_4}) – P({C_1} \cap {C_2} \cap {C_3} \cap {C_4})
\end{array}$$
که در آن:
$$\begin{array}{l}
P({C_1}) = {Q_A}{Q_B}\\
P({C_2}) = {Q_C}{Q_D}\\
P({C_3}) = {Q_A}{Q_D}{Q_E}\\
P({C_4}) = {Q_B}{Q_C}{Q_E}\\
P({C_1} \cap {C_2}) = P({C_1})P({C_2}) = {Q_A}{Q_B}{Q_C}{Q_D}\\
P({C_1} \cap {C_3}) = P({C_1})P({C_3}) = {Q_A}{Q_B}{Q_D}{Q_E}\\
P({C_1} \cap {C_4}) = P({C_1})P({C_4}) = {Q_A}{Q_B}{Q_C}{Q_E}\\
P({C_2} \cap {C_3}) = P({C_2})P({C_3}) = {Q_A}{Q_C}{Q_D}{Q_E}\\
P({C_2} \cap {C_4}) = P({C_2})P({C_4}) = {Q_B}{Q_C}{Q_D}{Q_E}\\
P({C_3} \cap {C_4}) = P({C_3})P({C_4}) = {Q_A}{Q_B}{Q_C}{Q_D}{Q_E}\\
P({C_1} \cap {C_2} \cap {C_3}) = P({C_1} \cap {C_2} \cap {C_4})\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = P({C_1} \cap {C_3} \cap {C_4})\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = P({C_2} \cap {C_3} \cap {C_4})\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = P({C_1} \cap {C_2} \cap {C_3} \cap {C_4})\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {Q_A}{Q_B}{Q_C}{Q_D}{Q_E}
\end{array}$$
بنابراین:
رابطه (4)
$$\begin{array}{l}
{Q_s} = {Q_A}{Q_B} + {Q_C}{Q_D} + {Q_A}{Q_D}{Q_E}\\
\,\,\,\,\,\,\,\,\, + {Q_B}{Q_C}{Q_E} - {Q_A}{Q_B}{Q_C}{Q_D}\\
\;\;\;\;\;\; - {Q_A}{Q_B}{Q_D}{Q_E} - {Q_A}{Q_B}{Q_C}{Q_E}\\
\,\,\,\,\,\,\,\,\, - {Q_A}{Q_C}{Q_D}{Q_E} - {Q_A}{Q_C}{Q_D}{Q_E}\\
\,\,\,\,\,\,\,\,\, - {Q_B}{Q_C}{Q_D}{Q_E} + 2{Q_A}{Q_B}{Q_C}{Q_D}{Q_E}
\end{array}$$
و با جایگذاری:
$$\begin{array}{l}
Q = 1 – R = 1 – 0.99 = 0.01\\
{Q_s} = 0.00020195\\
{R_s} = 1 – {Q_s} = 0.9997805
\end{array}$$
ملاحظه میشود که نتایج فوق منطبق بر همان نتایجی است که با روش احتمال شرطی به دست آمد.
ارزیابی تقریبی (Approximate Evaluation)
ارزیابی دقیق به روش محاسباتی فوق همواره از نظر تئوری میسر است ولی با بزرگ شدن سیستم کاری بسیار وقت‌گیر و خسته کننده میشود. برای رفع این مشکل روش‌های تقریبی به کار می‌رود که اگرچه قدری از میزان دقت می‌کاهد ولی ارزیابی را به مراتب سریع‌تر می‌کند. میزان عدم دقت، معمولاً ناچیز و در محدوده تغییرات مجاز اطلاعات مربوط به قابلیت اطمینان می‌باشد به ویژه که قابلیت اطمینان عضوهای سیستم معمولاً از مقادیر بزرگی برخوردار است.
ارزیابی تقریبی به دو طریق میسر است در طریق اول در محاسبه احتمال شکست از جمع احتمال مجموعه‌های انقطاع استفاده میشود:
رابطه (5)
$$\begin{array}{l}
{Q_s} = P({C_1}) + P({C_2}) + ... + P({C_i}) + ... + P({C_n})\\
\,\,\,\,\,\,\, = \sum\limits_{i = 1}^n {P({C_i})}
\end{array}$$
و لذا برای مثال فوق خواهیم داشت:
رابطه (6)
$${Q_s} = {Q_A}{Q_B} + {Q_C}{Q_D} + {Q_A}{Q_D}{Q_E} + {Q_B}{Q_C}{Q_E}$$
هرگاه: ${Q_A} = {Q_B} = {Q_C} = {Q_D} = {Q_E} = Q$، آنگاه:${Q_s} = 2{Q^2} + 2{Q^3}$
و به ازای $Q = 0.01$ خواهیم داشت:
$$\begin{array}{l}
{Q_s} = 0.000202\\
{R_s} = 0.999798
\end{array}$$
ارزیابی دقیق به روش محاسباتی فوق همواره از نظر تئوری میسر است ولی با بزرگ شدن سیستم کاری بسیار وقت‌گیر و خسته کننده میشود. برای رفع این مشکل روش‌های تقریبی به کار می‌رود که اگرچه قدری از میزان دقت می‌کاهد ولی ارزیابی را به مراتب سریع‌تر می‌کند. میزان عدم دقت، معمولاً ناچیز و در محدوده تغییرات مجاز اطلاعات مربوط به قابلیت اطمینان می‌باشد به ویژه که قابلیت اطمینان عضوهای سیستم معمولاً از مقادیر بزرگی برخوردار است.
ارزیابی تقریبی به دو طریق میسر است در طریق اول در محاسبه احتمال شکست از جمع احتمال مجموعه‌های انقطاع استفاده میشود:
ملاحظه میشود که در این مثال، خطای ارزیابی تقریبی محدود به $ + \% 0.02$ برای ${Q_s}$ و $ – \% 5 \times {10^{ – 66}}$ برای ${R_s}$ است. علی‌رغم کاهش قابل توجهی در حجم محاسبات، بی‌دقتی محاسبات بسیار ناچیز و قابل صرف نظر کردن است و همواره با این روش خطای نسبی برای ${Q_s}$ مثبت است.
در طریق دوم ارزیابی تقریبی، از مجموعه انقطاعی که تعداد عضوهای آن بیش از حد معینی است چشم‌پوشی میشود. تعداد عضوهای هر مجموعه، رسته آن را مشخص می‌کند. بنابراین فرض میشود که احتمال وقوع مجموعه انقطاع رسته بالا کوچک و قابل اغماض است و این فرضی است که صحت آن بستگی به میزان قابلیت اطمینان عضوها در مجموعه‌های انقطاع خواهد داشت.
وقتی همه اجزاء از قابلیت اطمینان زیاد و یکسانی برخوردار باشد فرض فوق صحیح است ولی هرگاه عضوهای مجموعه رسته پایین، قابلیت اطمینان زیاد ولی عضوهای مجموعه رسته بالا، قابلیت اطمینان کم داشته باشد موجب عدم صحت این فرض میشود. از این رو در استفاده از طریق دوم باید احتیاط کافی مبذول شود.
مجدداً در اعمال تقریب برای مثال (2) این دفعه از مجموعه‌های رسته سوم صرف نظر میشود و لذا برای احتمال شکست سیستم خواهیم داشت:
رابطه (7)
$${Q_s} = {Q_A}{Q_B} + {Q_C}{Q_D}$$
هرگاه:
رابطه (8)
$${Q_A} = {Q_B} = {Q_C} = {Q_D} = Q$$
$${Q_s} = 2{Q^2}$$
و به ازای $Q = 0.01$ خواهیم داشت:
$${Q_s} = 0.000200\;\;,\;\;\;{R_s} = 0.999800$$
در این مورد خطای نسبی محاسبات ${R_s}$ و ${Q_s}$ به ترتیب $ + \% 2 \times {10^{ – 4}}$ و $ – \% 1$ میشود و مقدار آن‌ها با افزایش قابلیت اطمینان عضوها، کمتر نیز میشود.
شناسایی مجموعه‌های انقطاع (Deducing the Minimal Cut Sets)
در این بحث اشاره شد که تشخیص مجموعه‌های انقطاع با بازبینی عینی میسر است. البته اجرای این روش برای سیستمهای ساده و کوچک با دشواری زیادی همراه نیست ولی برای سیستمهای پیچیده‌تر و بزرگ، کار دشواری می‌باشد. از این رو تعدادی روش‌های شناسایی ابداع شده است و حتی می‌توان از آن‌ها در برنامه‌نویسی رایانه‌ای نیز استفاده کرد. در اینجا به یکی از این روش‌ها که حداقل با کاربرد آن شناسایی دستی با سهولت میسر شود اشاره میشود.
در اکثر روش‌های شناسایی توجه ویژه‌ای به شناسایی مسیرهای کوتاه از ورودی به خروجی میشود. طبق تعریف زمانی میان ورودی و خروجی مسیری کوتاه محسوب میشود که در آن هر انشعابی با انشعابات دیگر بیش از یک بار تلاقی نداشته باشد طبق این تعریف مسیرهای $AED,\;BD,\;AC$ و $BEC$ مسیرهای کوتاه برای سیستم شکل (1) محسوب میشود.
الف- روش شماره 1: در این روش گام‌های در پی آمده برداشته میشود:
1- همه مسیرهای غیرتکراری مشخص شود.
2- آرایه وقوع برای شناسایی عضوهای هر مسیر تشکیل شود.
3- هرگاه همه اجزاء ستونی از آرایه وقوع غیرصفر باشد نمایانگر اجزای مجموعه انقطاع رسته اول خواهد بود.
4- ستون‌های آرایه وقوع دو به دو ملحق شود. در صورتی که همه اجزای ستون‌های ملحق شونده غیرصفر باشد، نمایانگر عضوهای مجموعه انقطاع رسته دوم خواهد بود. مجموعه‌های انقطاع رسته دومی که در بردارنده مجموعه‌های رسته اول هستند حذف می‌‌شوند به نحوی که مجموعه انقطاع‌های رسته دوم غیرتکراری حاصل شود.
5- مرحله چهارم برای هر سه ستون آرایه تکرار شود به نحوی که موجب حذف مجموعه انقطاع رسته سوم در بردارنده مجموعه‌های رسته اول و دوم گردد.
مثال (3): برای شکل (1) روش فوق به کار برده شود.
1- مسیرهای غیرتکراری $BEC,\;BD,\;AED,\;AC$ تشخیص داده میشود.
2- تشکیل آرایه وقوع:
3- هیچ یک از ستون‌های آرایه، به تنهایی اجزاء غیرصفر کامل ندارد. بنابراین مجموعه انقطاع رسته اول وجود ندارد.
4- همه اجزای ستون‌های الحاقی $A + B$ و همچنین $C + D$ غیرصفر است و لذا این دو ستون الحاقی، مجموعه‌های انقطاع رسته دوم را مشخص می‌نمایند و از آنجایی که مجموعه رسته اول وجود نداشت لذا این دو مجموعه، غیرتکراری است.
5- همه اجزای ستون‌های الحاقی سه‌گانه $BCD,\;ADE,\;ACD,\;ABE,\;ABD,\;ABC,\;CDE,\;BCE$ غیرصفر است و بنابراین مجموعه انقطاع رسته سوم را به دست می‌دهد. با حذف مجموعه‌های شامل $AB$ و $CD$، به مجموعه‌های انقطاع $BCE,\;ADE$ به عنوان مجموعه‌های رسته سوم غیرتکراری خواهیم رسید.
6- با آزمایش مجموعه‌های رسته بالاتر ملاحظه خواهد شد که هیچ یک غیرتکراری نیست و لذا کوچکترین مجموعه‌ها، مجموعه‌های انقطاع با کمترین عضوها شامل $BCE,\;ADE,\;CD,\;AB$ میشود، کما این که قبلاً هم چنین تعیین شده بود.
| مسیر | A | B | C | D | E |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 | 1 |
کاربرد و مقایسه شیوه‌های احتمال شرطی و مجموعه انقطاع (Application & Comparison of the Two Techniques)
دو شیوه احتمال شرطی و مجموعه انقطاع در حل مسئله دیگری (غیر از مسئله کلاسیک شبکه پل) با ذکر مثالی ارائه میشود.
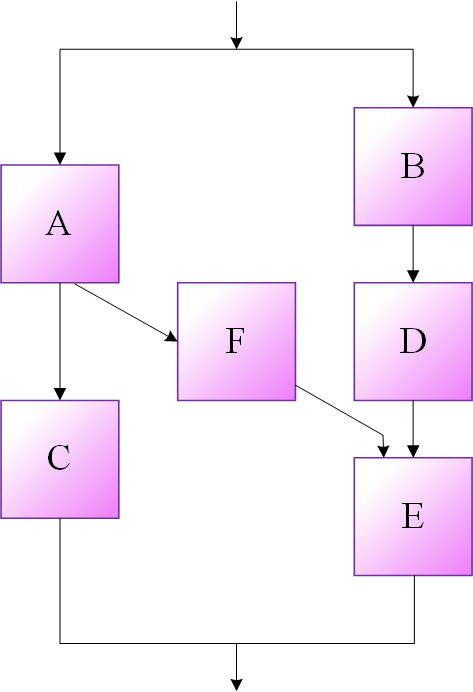
مثال (4): مطلوب است تعیین قابلیت اطمینان سیستم با شبکه‌ای مطابق شکل (4) مشروط بر آن که قابلیت اطمینان هر یک از عضوها برابر با 0.99 در نظر گرفته شود.
الف) شیوه احتمال شرطی:
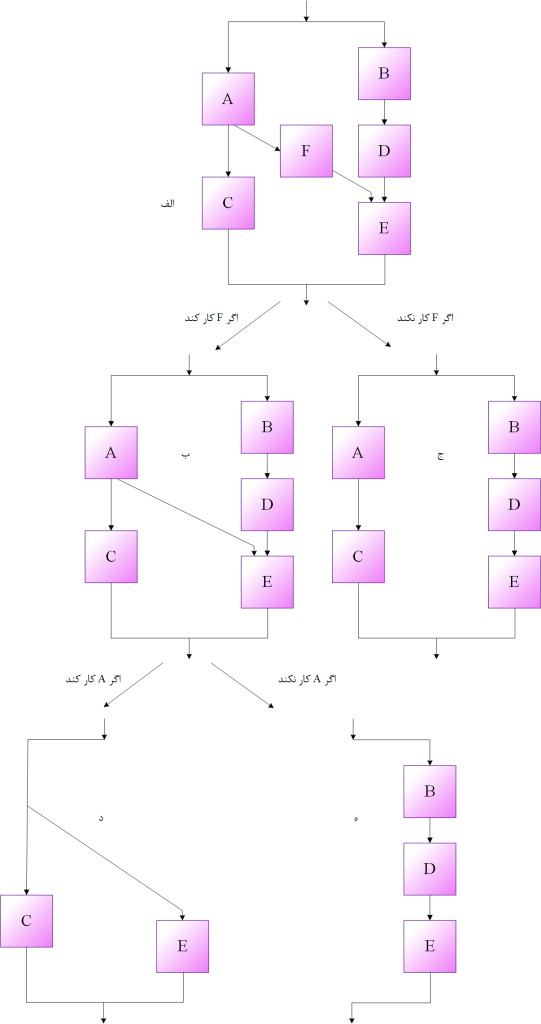
همان‌گونه که قبلاً توضیح داده شد برای کاهش حجم محاسبات، انتخاب عضو مناسبی از میان عضوهای سیستم مطرح می‌باشد. برای این منظور با انتخاب عضو $F$ زیرسیستم‌هایی مطابق شکل‌های (5)-ب، ج حاصل میشود. اگرچه زیرسیستم شکل (5)-ج متشکل از شبکه‌های متوالی ـ موازی و به سهولت تحلیل‌پذیر است ولی شبکه شکل (5)-ب مستلزم تجزیه بیشتری می‌باشد.
برای این منظور عضو $A$ انتخاب میشود و شرط عملکرد و شکست آن اعمال میشود بدین ترتیب شکل‌های (5)-د، هـ به دست می‌آید.
توجه شود که در شکل (5)-د عضوهای $B$ و $D$ ظاهر نمی‌شود زیرا $A$ دارای عملکرد صحیح است و بدون توجه به این که $D,\;B$ در چه شرایطی باشد ورودی برای $E$ تأمین میشود.
بنابراین قابلیت اطمینان سیستم بر مبنای حالات تجزیه فوق قابل تعیین خواهد بود.
$$\begin{array}{l}
{R_s} = {R_s}(if\,F\,is\,good){R_F} + {R_s}(if\,F\,is\,bad){Q_F}\\
{R_s}(if\,F\,is\,bad) = 1 – (1 – {R_B}{R_D}{R_E})(1 – {R_A}{R_C})\\
{R_s}(if\,F\,is\,good) = {R_s}(if\,A\,is\,good){R_A}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {R_s}(if\,A\,is\,bad){Q_A}\\
{R_s}(if\,A\,is\,good) = 1 – {Q_C}{Q_E}\\
{R_s}(if\,A\,is\,bad) = {R_B}{R_D}{R_E}
\end{array}$$
و با جایگذاری پارامترها خواهیم داشت:
$$\begin{array}{l}
{R_s} = [(1 – {Q_C}{Q_E}){R_A} + {R_B}{R_D}{R_E}{Q_A}]{R_F}\\
\;\;\;\;\;\; + [1 – (1 – {R_B}{R_D}{R_E})(1 – {R_A}{R_C})]{Q_F}
\end{array}$$
و با جایگذاری عددی:
$${R_s} = 0.999602\;\;\;,\;\;\;{Q_s} = 0.000398$$
ب) شیوه مجموعه انقطاع:
کوچکترین مجموعه‌های انقطاع در شبکه شکل (4) با کاربرد روش بازبینی عینی و شناسایی مجموعه‌های غیرتکراری عبارت است از:
$$(AB),\;(AD),\;(AE),\;(CE),\;(BCF),\;(CDF)$$
محاسبه دقیق قابلیت اطمینان سیستم به روش دستی بسیار پرزحمت و وقت‌گیر میشود زیرا با حضور تعداد 6 مجموعه انقطاع در معادله دقیق تعداد 63 ترم مطرح خواهند بود. بنابراین منطقی آن است که با کاربرد روش محاسبه تقریبی ضمناً مقایسه‌ای با نتیجه حاصله از روش احتمال شرطی صورت گیرد.
در ابتدا نتیجه را صرفاً بر مبنای مجموعه‌های رسته دوم به دست می‌آوریم که در آن مجموع احتمال مجموعه‌های انقطاع مطرح میشود:
$$\begin{array}{l}
{Q_s} = {Q_A}{Q_B} + {Q_A}{Q_D} + {Q_E}{Q_A} + {Q_C}{Q_E}\\
\;\;\;\; = 0.000400\\
\;\;\;\;{R_s} = 0.999600
\end{array}$$
که خطای نسبی معادل 0.5% در مقدار احتمال شکست سیستم و معادل 0.0002%- در برآورد مقدار قابلیت اطمینان سیستم به وجود می‌آید. حال با در نظر گرفتن احتمال مجموعه‌های رسته سوم خواهیم داشت:
$$\begin{array}{l}
{Q_s} = {Q_A}{Q_B} + {Q_A}{Q_D} + {Q_A}{Q_E} + {Q_C}{Q_E}\\
\,\,\,\,\,\, + {Q_B}{Q_C}{Q_F} + {Q_C}{Q_D}{Q_F}\\
\;\;\;\; = 0.000402\\
\;\;\;\;{R_s} = 0.999598
\end{array}$$
در این حالت خطای نسبی معادل 1.0%+، 0.0004%- به ترتیب در مقادیر احتمال شکست و قابلیت اطمینان به دست می‌دهد. همان‌گونه که روش ارزیابی تقریبی با استفاده از شیوه مجموعه انقطاع در اینجا پاسخ قابل قبولی به دست داد در اکثر کاربردها دقت کافی به دست می‌دهد.
وضعیت‌های چندگانه شکست (Multi-Failure Modes)
در سراسر این بحث فرض بر کاربرد عضوهایی بوده است که صرفاً یک وضعیت شکست دارند و یا به عبارت دیگر صرفاً دارای دو وضعیت یکی عملکرد و دیگری شکست هستند. مثال‌های متعددی مبیّن عدم کفایت این نوع نمایش برای عضوهای سیستم واقعی است.
به عنوان یکی از موارد کلی، عضوهایی را می‌توان مثال زد که عملکردی بر اساس دستور دریافتی دارند و شکست آن‌ها در دو وضعیت قبل و پس از دریافت دستور می‌تواند رخ دهد. به عنوان مثال دیگر، عضوهایی مطرح است که شکست آن‌ها به دو گونه مختلف در حالت‌های باز و بسته اتفاق می‌افتد. بسیاری از اجزاء و ادوات الکترونیکی مانند دیودها، نیمه‌هادی‌ها، ترانسفورمرها، کابل‌ها و مانند آن‌ها از این نوع است. به منظور ارزیابی صحیح و واقعی قابلیت اطمینان سیستم‌هایی که دارای چنین عضوهایی است همه وضعیت‌های شکست باید در نظر گرفته شود. اگرچه طرق مختلفی برای این منظور ابداع شده است ولی در اینجا تنها به ذکر دو طریق برای تحلیل سیستمی متشکل از دیودها می‌پردازیم.
مثال (5): مطلوب است تحلیل پارامتری، برای احتمال عملکرد صحیح سیستم نشان داده در شکل (6) مشروط بر آن که ایجاد مسیر یک طرفه برای جریان الکتریکی مطلوب نظر باشد.
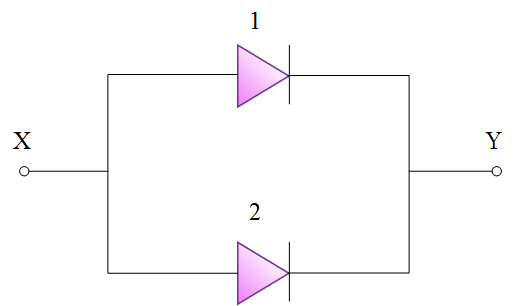
احتمال حالت‌های مختلف برای دیودها یکسان و با تعریف زیر در نظر گرفته میشود:
${P_n}$ احتمال عملکرد عادی و صحیح
${P_o}$ احتمال شکست به صورت قطع جریان
${P_s}$ احتمال شکست به صورت اتصال کوتاه
الف) برشمردن حالت‌ها: با کاربرد توزیع دوجمله‌ای، احتمال حالت‌های مختلف بر اساس بسط دوجمله‌ای ${(R + Q)^n}$ به دست می‌آید که در آن $R$ و $Q$ احتمال عملکرد صحیح و وقوع شکست با حاصل جمعی برابر واحد و $n$ تعداد اجزاء می‌باشد. در این مثال احتمال حالت‌ها عبارتند از: ${P_o}،{P_n}$ و ${P_s}$ که مجموعی برابر واحد دارند. بنابراین در کاربرد توزیع دوجمله‌ای به جای دو جمله، می‌توان این سه جمله را جایگزین نمود و احتمال حالت‌های مختلف را با بسط جملات ${({P_n} + {P_o} + {P_s})^n}$ تعیین کرد و در صورت تفاوت احتمال حالت‌های عضوها:
$$\begin{array}{l}
({P_{{n_1}}} + {P_{{o_1}}} + {P_{{s_1}}})({P_{{n_2}}} + {P_{{o_2}}} + {P_{{s_2}}})\\
\,\,\,\,…({P_{{n_i}}} + {P_{{o_i}}} + {P_{{s_i}}})…
\end{array}$$
و حال:
$$\begin{array}{l}
{({P_n} + {P_o} + {P_s})^2} = P_n^2 + P_o^2 + P_s^2\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2{P_n}{P_o} + 2{P_n}{P_s} + 2{P_o}{P_s}
\end{array}$$
در این مرحله باید تشخیص داد که کدام یک از جملات فوق نمایانگر وضعیت عملکرد صحیح سیستم $G$ و کدام یک معرف وقوع شکست $B$ است. سپس با جمع کردن نتایج محاسبه جملات مشخص شده با حرف $G$ قابلیت اطمینان سیستم تعیین میشود و احتمال وقوع شکست از جمع ترم‌های مشخص شده با حرف $B$ به دست می‌آید. بنابراین:
$$\begin{array}{l}
{R_s} = P_n^2 + 2{P_n}{P_o}\\
{Q_s} = P_o^2 + P_s^2 + 2{P_n}{P_s} + 2{P_o}{P_s}
\end{array}$$
هرگاه ${P_o} = {P_s} = 0.01,\;{P_n} = 0.98$ باشد در این صورت:$$\begin{array}{l}
{R_s} = 0.98\\
{Q_s} = 0.02
\end{array}$$
1)
$${P_o} = 0\;\;\;\;\;\;\;\;{P_s} = 0.02\;\; \to \;\;{R_s} = 0.9604$$
2)
$${P_o} = 0.02\;\;\;\;\;\;\;{P_s} = 0\;\; \to \;\;{R_s} = 0.9996$$
در نتیجه هرگاه ${P_s} > {P_o}$ باشد قابلیت اطمینان سیستم مورد بحث متشکل از دو دیود، نسبت به یک دیود کمتر است اما در چنین سیستمی وقتی که ${P_s} < {P_o}$ باشد قابلیت اطمینان آن نسبت به یک دیود بیشتر خواهد بود.
ب) احتمال شرطی: با کاربرد معادله احتمال شرطی خواهیم داشت:
$$\begin{array}{l}
{R_s} = P(sys\;S|one\;is\;normal)P(one\;is\;normal)\\
\;\;\;\;\;\;\; + P(sys\;S|one\;is\;open)P(one\;is\;open)\\
\;\;\;\;\;\;\; + P(sys\;S|one\;is\;shorted)P(one\;is\;shorted)\\
\;\;\;\;\;\;\;given\;\;\;\;\;one\;is\;normal\;P(sys\;S) = {P_n} + {P_o}\\
\;\;\;\;\;\;\;given\;\;\;\;\;one\;is\;open\;P(sys\;S) = {P_n}\\
\;\;\;\;\;\;\;given\;\;\;\;\;one\;is\;shorted\;P(sys\;S) = 0
\end{array}$$
بنابراین:
$${R_s} = ({P_n} + {P_o}){P_n} + {P_n}{P_o} + o \times {P_s} = P_n^2 + 2{P_n}{P_o}$$
همچنین معادله احتمال شرطی برای بررسی احتمال شکست سیستم را نیز می‌توان تنظیم کرد.
در ضمن با روش‌های ابتکاری و کاربرد مفاهیم بنیادی می‌توان احتمال شکست سیستم را تعیین نمود. سیستم به دو طریق قطع جریان و اتصال کوتاه دچار شکست میشود و این طرق دو به دو ناسازگار است لذا:
$$\begin{array}{l}
P(system{\rm{ }}failing{\rm{ }}in{\rm{ }}the{\rm{ }}open{\rm{ }}circuit{\rm{ }}mode)\\
\,\,\,\,\, = {P_o}.{P_o} = P_o^2\\
P(system{\rm{ }}failing{\rm{ }}in{\rm{ }}the{\rm{ }}short{\rm{ }}circuit{\rm{ }}mode)\\
\,\,\,\,\, = {P_s} + {P_s} – {P_s}{P_s}
\end{array}$$
مانند قبل $\begin{array}{l}
P(system{\rm{ }}failure) = P_o^2 + 2{P_s} – P_s^2\\
{Q_s} = 0.02
\end{array}$ محاسبه میشود.
مثال (6): مطلوب است تعیین عبارت پارامتری در تعیین قابلیت اطمینان سیستمی مطابق شکل (7)، هرگاه تأمین مسیر یک طرفه برای جریان بین $X$ و $Y$ مطلوب نظر باشد، احتمال حالت‌های عملکرد دیودها همان است که در مثال (5) ارائه شد.
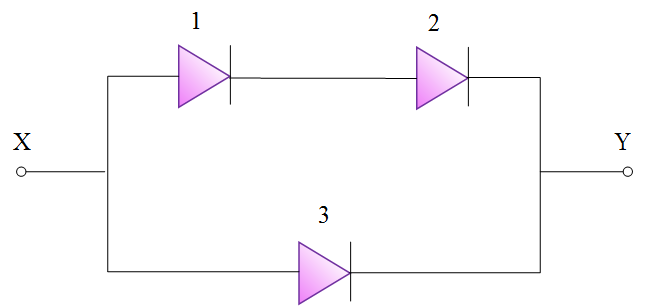
مجموعه دیودهای 1 و 2 را با حرف $A$ نشان می‌دهیم:
$$\begin{array}{l}
{R_s} = P(sys\;S|A\;is\;normal).P(A\;is\;normal)\\
\;\,\;\;\;\;\; + P(sys\;S|A\;is\;open).P(A\;is\;open)\\
\;\,\;\;\;\;\; + P(sys\;S|A\;is\;shorted).P(A\;is\;shorted)\\
\;\;\;\;\;\;\;given\;A\;is\;normal\;\;\;\;\;P(sys\;S) = {P_n} + {P_o}\\
\;\;\;\;\;\;\;given\;A\;is\;open\;\;\;\;\;\;\;P(sys\;S) = {P_n}\\
\;\;\;\;\;\;\;given\;A\;is\;shorted\;\;\;\;P(sys\;S) = 0
\end{array}$$
در نتیجه:
$$\begin{array}{l}
{R_s} = ({P_n} + {P_o}).P(A\;is\;normal)\\
\,\,\,\,\,\,\,\,\,\, + {P_n}.P(A\;is\;open) + 0 \times P(A\;is\;shorted)
\end{array}$$
همچنین با برشمردن حالت‌ها از بسط احتمالات سه‌گانه برای $A$ که متشکل از اجزای 1 و 2 می‌باشد، خواهیم داشت:
$$\begin{array}{l}
{({P_n} + {P_o} + {P_s})^2} = P_n^2 + P_o^2 + P_s^2\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2{P_n}{P_o} + 2{P_n}{P_s} + 2{P_o}{P_s}
\end{array}$$
و این عبارتی است که قبلاً نیز در مثال (5) به دست آورده شد. زیرا که صرفاً دو جزء در آن مطرح است ولی با توجه به متوالی بودن دیودهای 1 و 2 تشخیص جدیدی از شرایط عمل $A$ باید صورت گیرد. مجدداً با کاربرد حروف $O,\;N$ و $S$ معرف وضعیت عادی، قطع جریان و اتصال کوتاه، احتمالات مختلف شرایط عمل $A$ به دست می‌آید:
$$\begin{array}{l}
P(A\;is\;normal) = P_n^2 + 2{P_n}{P_s}\\
P(A\;is\;open) = P_o^2 + 2{P_n}{P_o} + 2{P_o}{P_s}\\
P(A\;is\;shorted) = P_s^2\\
{R_s} = ({P_n} + {P_o})(P_n^2 + 2{P_n}{P_s})\\
\,\,\,\,\,\, + {P_n}(P_o^2 + 2{P_n}{P_o} + 2{P_o}{P_s}) + 0 \times P_s^2\\
\;\;\;\; = P_n^3 + 2P_n^2{P_s} + 3P_n^2{P_o} + {P_n}P_o^2 + 4{P_n}{P_s}{P_o}
\end{array}$$
به طریقی مشابه می‌توان برای تعیین احتمال شکست سیستم ${Q_s}$ عمل نمود. در اینجا با منظور کردن ${P_o} = {P_s} = 0.01\;\;\;,\;\;\;{P_n} = 0.98$
${R_s} = 0.989702$
و در شرایط حدی هرگاه:
$${P_o} = 0\;\;\& \;\;{P_s} = 0.02\;\;\;\;\;\;\;\;{R_s} = 0.979608$$
هرگاه:
$${P_s} = 0\;\;\& \;\;{P_o} = 0.02\;\;\;\;\;\;\;\;{R_s} = 0.999208$$
برخی مقایسه‌ها میان نتایج مثال‌های (5) و (6) به شرح در پی آمده قابل ذکر می‌باشد:
1- قابلیت اطمینان سیستم با سه دیود در شرایط برابری احتمال شکست‌های قطع جریان و اتصال کوتاه از یک دیود تنها و همچنین از دو دیود موازی بیشتر است.
2- قابلیت اطمینان سیستم با سه دیود در شرایط احتمال صفر برای قطع جریان از دو دیود موازی، بیشتر ولی همچنان از یک دیود تنها کوچکترست.
3- قابلیت اطمینان سیستم با سه دیود در شرایط احتمال صفر برای اتصال کوتاه از دو دیود موازی، کمتر ولی از یک دیود تنها بیشتر است.
نتیجه‌گیری جالبی از مقایسه فوق به دست می‌آید بدین صورت که نمی‌توان بدون بررسی‌های لازم، مستقیماً فرض کرد که افزایش تعداد اجزاء موازی موجب افزایش قابلیت اطمینان سیستم میشود و یا افزایش تعداد اجزاء متوالی موجب کاهش قابلیت اطمینان سیستم میشود.