مدلسازی شبکه و ارزیابی سیستمهای ساده
تعداد بازدید: 2844
زمان مطالعه: 16 دقیقه
فهرست مطالب این نوشته
مفاهیم مدلسازی شبکه (Network Modelling Concepts)
قبل از کاربرد شیوه‌های تحلیل شبکه‌ها برای ارزیابی قابلیت اطمینان آن‌ها ضرورتاً باید درک کاملی از روابط میان سیستم و مدلسازی شبکه برای آن حاصل باشد. در وهله نخست باید توجه شود که یک سیستم واقعی و شبکه وابستگی قابلیت اطمینان از نظر ساختار جانمایی عضوهای آن الزاماً همانند نیست. به همین دلیل قبلاً نیز تأکید شد که برای یک تحلیل‌گر قابلیت اطمینان باید درک کاملی از عملکردها و الزامات یک سیستم حاصل شده باشد تا امکان بررسی‌های کمّی برای وی فراهم شود.
در اینجا به تعریف‌هایی از شبکه وابستگی عضوها به صورت متوالی و موازی در تشکیل سیستم می‌پردازیم:
الف: سیستمهای با شبکه متوالی: از دیدگاه قابلیت اطمینان برای عملکرد صحیح یک سیستم با شبکه متوالی باید همه عضوهای آن در حال کار باشد و بنابراین از کار افتادن هر یک از عضوها موجب از کار افتادن سیستم می‌شود.
ب: سیستمهای با شبکه موازی: از دیدگاه قابلیت اطمینان هرگاه فقط یکی از عضوهای سیستمی با شبکه موازی سالم باشد سیستم همچنان دارای عملکرد انتظاری خواهد بود و بنابراین فقط زمانی که کلیه عضوها از کار بیفتد موجب از کار افتادن سیستم می‌شود.
این تعریف‌ها زمینه‌ای برای ارتباط با بحث توزیع دوجمله‌ای فراهم می‌آورد. یک سیستم متوالی عبارت از سیستمی بدون عضو مازاد و یک سیستم موازی عبارت از سیستمی با کلیه عضوهای مازاد می‌باشد.
شبکه وابستگی متوالی و موازی از متداول‌ترین و ساده‌ترین ارتباط‌های میان عضوها در تشکیل یک سیستم با سطوح مختلفی از پیچیدگی است و برای تحلیل آن‌ها نیاز به شیوه‌های ویژه‌ای می‌باشد. نمایش شبکه قابلیت اطمینان با استفاده از نمودار جعبه‌ای صورت می‌گیرد.
سیستمهای با شبکه متوالی (Series Systems)
سیستمی متشکل از عضوهای مستقل با اتصال متوالی از دیدگاه قابلیت اطمینان در شکل (1) نمایش داده شده است. ترتیب ارائه شده نمایانگر ضرورت عملکرد صحیح هر دو عضو برای حصول عملکرد صحیح سیستم است.
در صورتی که ${R_B},\;{R_A}$ احتمال عملکرد صحیح و ${Q_B},\;{Q_A}$ احتمال از کار افتادن این عضوها باشد از آنجایی که موفقیت و شکست، پدیده‌های دو به دو ناسازگار و مکمل است لذا:
$${R_A} + {Q_A} = 1\;\;\;,\;\;\;{R_B} + {Q_B} = 1$$
با کاربرد قواعد احتمال، احتمال عملکرد صحیح سیستم ${R_s}$ و یا به عبارتی دیگر قابلیت اطمینان آن:
رابطه (1)
$${R_s} = {R_A}\;.\;{R_B}$$
و در صورتی که تعداد $n$ عضو با شبکه متوالی مطرح باشد:
رابطه (2)
$${R_s} = \prod\limits_{i = 1}^n {{R_i}} $$
این معادله همچنین با نام قاعده ضرب قابلیت اطمینان شناخته می‌شود.
در برخی از کاربردها ترجیحاً ارزیابی نااطمینانی و یا به عبارتی احتمال از کار افتادن مورد توجه قرار می‌گیرد.
با توجه به این که موفقیت و شکست سیستم نیز دو حادثه مکمل است لذا برای احتمال از کار افتادن سیستم ${Q_s}$ داریم:
رابطه (3)
$${Q_s} = 1 - {R_A}\;.\;{R_B}$$
رابطه (4)
$${R_s} = \prod\limits_{i = 1}^n {{R_i}} $$
و برای $n$ عضو در تشکیل سیستم با شبکه متوالی خواهیم داشت:
رابطه (5)
$${Q_s} = 1 - \prod\limits_{i = 1}^n {{R_i}} $$
معادله (4) را بر مبنای مفهوم از کار افتادن سیستم به علت از کار افتادن $A$ یا $B$ و یا هر دو نیز می‌توان به دست آورد.
مثال (1): سیستمی متشکل از 10 عضو متناظر با شبکه وابستگی متوالی برای عملکرد صحیح می‌باشد. مطلوب است تعیین قابلیت اطمینان سیستم در صورتی که قابلیت اطمینان هر عضو معادل 95/0 در نظر گرفته شود.
$${R_s} = {0.95^{10}} = 0.5987$$
با این مثال ساده ملاحظه می‌شود که به طور کلی قابلیت اطمینان سیستم با شبکه وابستگی متوالی کمتر از قابلیت اطمینان هر یک از عضوهای آن می‌باشد و با افزایش تعداد عضوها کمتر هم می‌شود.
مثال (2): مطلوب است تعیین احتمال از کار افتادن سیستمی متشکل از دو عضو متوالی هر یک با قابلیت اطمینان 99/0.
از معادله (2) می‌توان نوشت:
$${Q_s} = 1 - {0.99^2} = 0.0199$$
$${Q_s} = 0.01 + 0.01 - (0.01 \times 0.01) = 0.0199$$
همچنین اگرچه هر دو روش حل، پاسخ‌های یکسانی طبق انتظار به دست می‌دهد ولی در برخی موارد از روش دوم و با اغماض از جمله سوم برای محاسبه تقریبی سریع استفاده می‌شود برای مثال:
$${Q_s} = 0.01 + 0.01 = 0.02$$
که صرفاً خطایی معادل 0.5% در بر خواهد داشت.
این روش تقریبی فقط برای تعداد عضوهای کم با قابلیت اطمینان‌‌های زیاد و آن هم با احتیاط لازم قابل توصیه می‌باشد. لذا با این روش تقریبی می‌توان گفت نااطمینانی سیستم مجموع نااطمینانی عضوهای آن است و قابلیت اطمینان سیستم، حاصلضرب قابلیت اطمینان عضوهای آن می‌باشد.
مثال (3): مطلوب است تعیین کمترین قابلیت اطمینان هر یک از 200 عضو متناظری که با شبکه متوالی، سیستمی با قابلیت اطمینان کل 0.99 به وجود آورند.
$${Q_s} = 0.01 + 0.01 = 0.02$$
$$R = {0.99^{\frac{1}{{200}}}} = 0.99995$$
سیستمهای با شبکه موازی (Parallel Systems)
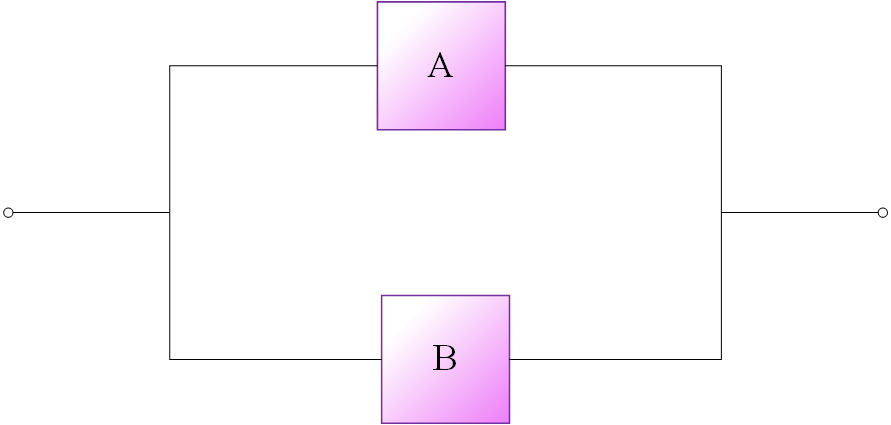
سیستمی متشکل از عضوهای مستقل با اتصال موازی از دیدگاه تحلیل قابلیت اطمینان در شکل (2) نمایش داده شده است. در این مورد برای حصول عملکرد صحیح سیستم کافی است تا فقط یکی از عضوها دارای عملکرد صحیح باشد.
با کاربرد قاعده‌های احتمال، این دفعه احتمال عملکرد صحیح سیستم ${R_p}$ را بر مبنای احتمال از کار افتادن عضوها با سهولت بیشتری می‌توان به دست آورد زیرا که از کار افتادن سیستم صرفاً در شرایط از کار افتادن همزمان عضوها ایجاد می‌شود.
رابطه (6)
$${Q_s} = 1 - {R_A}\;.\;{R_B}$$
رابطه (7)
$$\begin{array}{l}
{R_p} = 1 - (1 - {R_A})(1 - {R_B})\\
\,\,\,\,\,\,\, = {R_A} + {R_B} - {R_A}{R_B}
\end{array}$$
و برای تعداد $n$ عضو در تشکیل سیستم با شبکه موازی:
رابطه (8)
$${R_p} = 1 - \prod\nolimits_{i = 1}^n {{Q_i}} $$
رابطه (9)
$${Q_p} = {Q_A}\;.\;{Q_B}$$
رابطه (10)
$${Q_p} = \prod\limits_{i = 1}^n {{Q_i}} $$
مثال (4): مطلوب است تعیین قابلیت اطمینان و احتمال از کار افتادن سیستمی با عضوهای موازی و دارای قابلیت اطمینان 0.99، 0.95، 0.98، 0.97
با استفاده از معادله (10) داریم:
$$\begin{array}{l}
{Q_p} = (1 - 0.99)(1 - 0.95)(1 - 0.98)(1 - 0.97)\\
\,\,\,\,\,\,\, = 3 \times {10^{ - 7}}
\end{array}$$
و با استفاده از معادله (8) داریم:
$${R_p} = 1 - 3 \times {10^{ - 7}} = 0.9999997$$
از این مثال ملاحظه می‌شود که چگونه کاربرد فیزیکی قابلیت اطمینان $R$ در موارد عملی همراه با دشواری‌های اجرایی به علت حضور تعداد زیاد رقم 9 پس از اعشار است و از این رو ترجیحاً از مقدار نااطمینانی در بیان قابلیت اطمینان استفاده می‌شود.
مثال (5): مطلوب است ارزیابی قابلیت اطمینان سیستمی متشکل از عضوهایی با قابلیت اطمینان 0.8 در یک شبکه موازی، هرگاه از تعداد عضوهای بیشتری استفاده شود.
مطابق جدول (1) با افزایش تعداد عضوها از 1 به 6 قابلیت اطمینان سیستم و میزان افزایش آن در هر مرحله تحت عنوان تغییرات پله‌ای قابلیت اطمینان ارائه شده است. همچنین درصد مقایسه‌ای این تغییرات نسبت به یک عضو واحد در تشکیل سیستم محاسبه و ارائه شده است.
جدول (1): نتایج قابلیت اطمینان برای مثال (5)
| تعداد عضوها | قابلیت اطمینان سیستم | مقدار افزایش قابلیت اطمینان | درصد نسبی افزایش قابلیت اطمینان |
|---|---|---|---|
| 1 | 0.8 | - | - |
| 2 | 0.96 | 0.16 | 20.0 |
| 3 | 0.992 | 0.032 | 24.0 |
| 4 | 0.998 | 0.0064 | 24.8 |
| 5 | 0.99968 | 0.00128 | 24.96 |
| 6 | 0.999936 | 0.000256 | 24.99 |
مثال (6): مطلوب است تعیین کمترین تعداد عضوها در یک شبکه موازی که هر یک با قابلیت اطمینان 0.7، سیستمی با قابلیت اطمینان 0.999 ایجاد کند.
با استفاده از معادله (10) داریم:
$$\begin{array}{l}
1 - 0.999 = {(1 - 0.7)^n}\\
0.001 = {0.3^n}\\
n = 5.74
\end{array}$$
چون تعداد صرفاً عددی صحیح می‌تواند اختیار کند لذا کمترین تعداد عضوهای لازم برابر 6 باید اختیار شود.
سیستمهای با شبکه متوالی ـ موازی (Series-Parallel Systems)
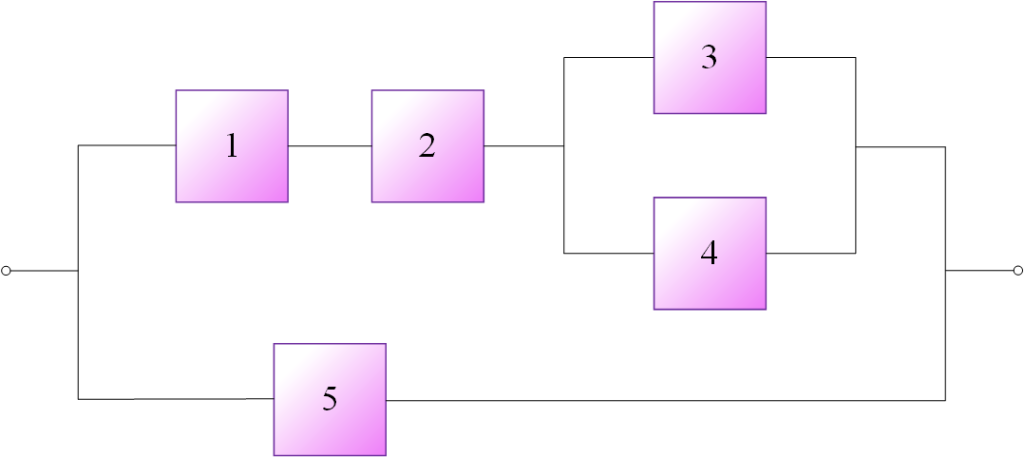
مثال (7): با تعیین عبارت پارامتری در محاسبه قابلیت اطمینان سیستم ترکیبی مطابق شکل (3) به ازای قابلیت اطمینان هر عضو برابر 0.9، قابلیت اطمینان سیستم را به دست آورید.
$$\begin{array}{l}
{R_{11}} = 1 - (1 - {R_9})(1 - {R_{10}})\\
\,\,\,\,\,\,\,\, = {R_9} + {R_{10}} - {R_9}{R_{10}}\\
\;\;\;\;\; = {R_1}{R_2}{R_3}{R_4} + {R_5}{R_6}{R_7}{R_8}\\
\,\,\,\,\,\,\, - {R_1}{R_2}{R_3}{R_4}{R_5}{R_6}{R_7}{R_8}
\end{array}$$
بر مبنای اطلاعات مسئله:
$${R_{11}} = {0.9^4} + {0.9^4} + {0.9^8} = 0.8817$$
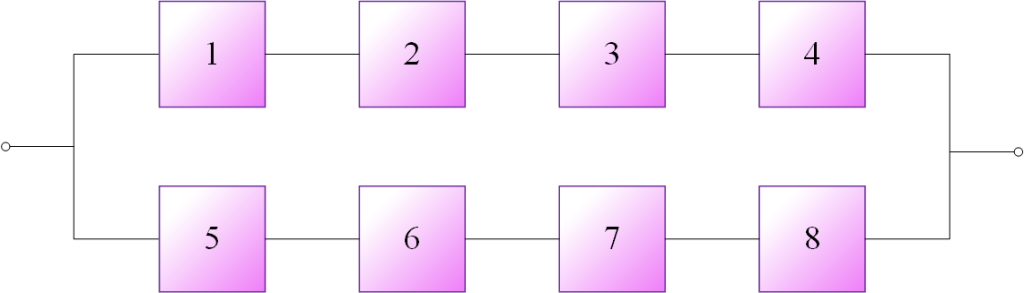
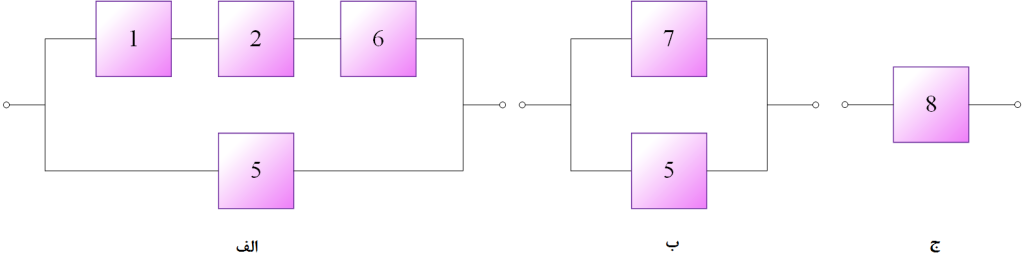
مثال (8): با تعیین عبارت پارامتری در محاسبه نااطمینانی سیستم ترکیبی مطابق شکل (4) به ازای قابلیت اطمینان هر عضو برابر با 0.8 میزان نااطمینانی سیستم را به دست آورید.
هرگاه ${R_1}$ تا ${R_5}$ و همچنین ${Q_1}$ تا ${Q_5}$ به ترتیب قابلیت اطمینان و نااطمینانی عضوهای شماره 1 تا 5 باشد در این صورت:
$$\begin{array}{l}
{Q_6} = {Q_3}{Q_4}\\
{Q_7} = 1 - (1 - {Q_1})(1 - {Q_2})(1 - {Q_6})\\
{Q_{sys}} = {Q_5}\;.\;{Q_7}\\
\;\;\;\;\;\; = {Q_5}({Q_1} + {Q_2} + {Q_3}{Q_4} - {Q_1}{Q_2}\\
\;\;\;\;\;\; - {Q_2}{Q_3}{Q_4} - {Q_3}{Q_4}{Q_1} + {Q_1}{Q_2}{Q_3}{Q_4})
\end{array}$$
به ازای ${R_i} = 0.8\;$ و ${Q_i} = 0.2$ مقدار ${Q_{sys}} = 0.07712$ محاسبه می‌شود.
روش دیگر:
$$\begin{array}{l}
{R_6} = {R_3} + {R_4} - {R_3}{R_4}\\
{R_7} = {R_1}{R_2}{R_6}\\
{R_{sys}} = {R_5} + {R_7} - {R_5}{R_7}\\
\;\;\;\;\;\; = {R_5} + {R_1}{R_2}({R_3} + {R_4} - {R_3}{R_4})\\
\;\;\;\;\;\; - {R_5}{R_1}{R_2}({R_3} + {R_4} - {R_3}{R_4})
\end{array}$$
به ازای ${R_i} = 0.8$ مقادیر محاسبه شده به شرح زیر هستند:
$${R_{sys}} = 0.92288$$
یا:
$${Q_{sys}} = 1 – 0.92288 = 0.07712$$
سیستمهای با برخی عضوهای مازاد (Partially Redundant Systems)
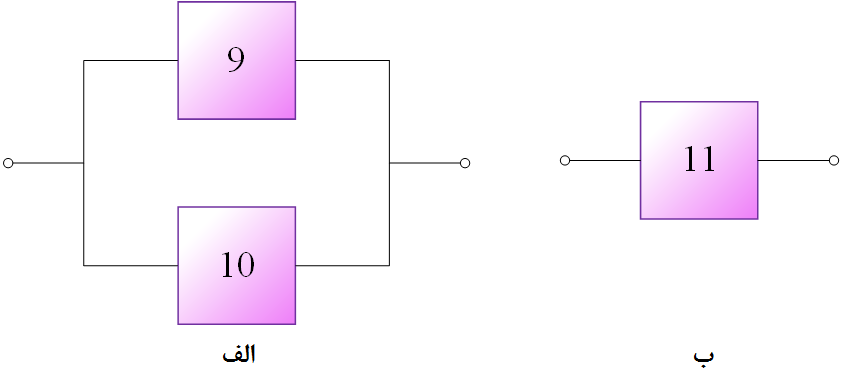
مثال (9): مطلوب است تعیین عبارت پارامتری در محاسبه نااطمینانی سیستمی مطابق نمودار شکل (7) مشروط بر آن که همه انشعابات موازی مبیّن مازاد کامل باشد به جز شاخه مشخص با سه جزء 4، 5 و 6 که به دو جزء از آن‌ها برای عملکرد صحیح این قسمت از سیستم نیاز می‌باشد.
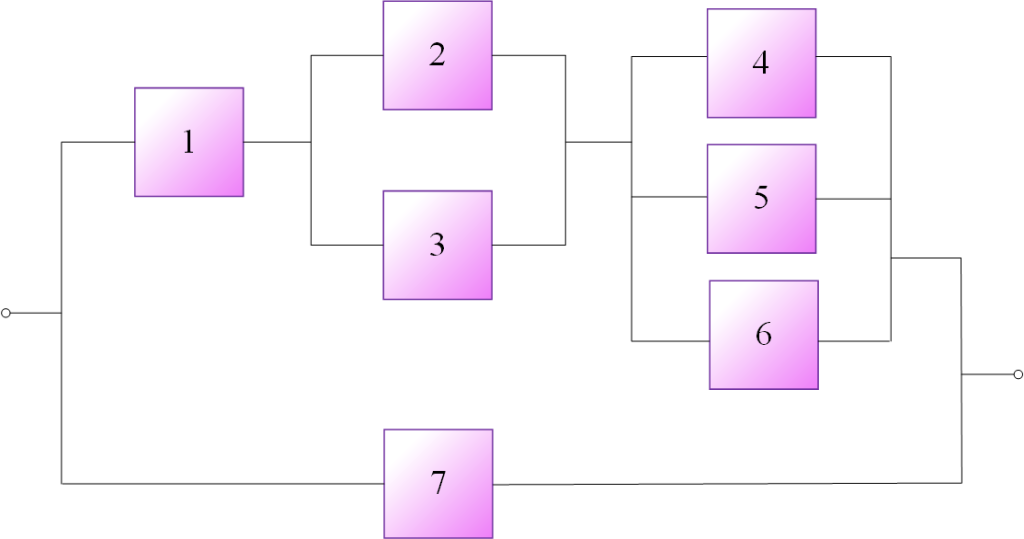
اصول معادل‌سازی در ساده کردن نمودار این سیستم کاربردپذیر است و لذا عضوهای 2 و 3 با عضو معادل 8 و عضوهای 4، 3 و 6 با عضو معادل 9 جایگذاری گشته و سپس برای عضوهای 1، 8 و 9 عضو معادل 10 در نظر گرفته و نهایتاً واحد معادل 11 برای عضوهای 10 و 7 معادل سیستم را به دست می‌دهد (شکل (8)).
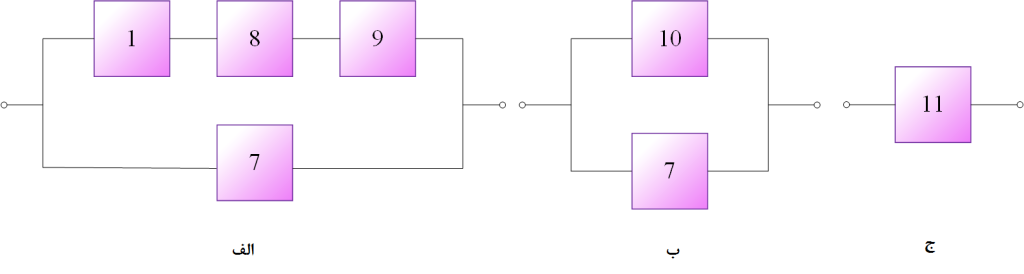
تنها اختلاف اساسی میان این مثال با مثال‌های پیشین در این بحث تغییر قابلیت اطمینان عضو معادل 9 است. برای این منظور از مفاهیم توزیع دوجمله‌ای استفاده می‌شود و در صورتی که عضوهای 4، 5 و 6 متناظر باشد این کار مستقیماً قابل اجرا است. مجدداً در صورتی که ${R_1}$ تا ${R_7}$ و ${Q_1}$ تا ${Q_7}$ به ترتیب نمایانگر قابلیت اطمینان و نااطمینانی عضوهای شماره 1 تا 7 باشد:
$${Q_8} = {Q_2}{Q_3}$$
$${R_{10}} = {R_1}{R_8}{R_9}$$
$$\begin{array}{l}
{Q_{11}} = {Q_{10}}{Q_7}\\
\;\;\;\;\; = {Q_7}(1 - {R_1}{R_8}{R_9})\\
\;\;\;\;\; = {Q_7}(1 - {R_1}(1 - {Q_2}{Q_3}){R_9})\\
\;\;\;\;\; = {Q_7}(1 - {R_1}{R_9} + {R_1}{R_9}{Q_2}{Q_3})
\end{array}$$
و در تعیین ${R_9}$ با استفاده از توزیع دوجمله‌ای برای عضوهای شماره 4، 5 و 6 خواهیم داشت:
$${R_4} = {R_5} = {R_6} = R$$
$${Q_4} = {Q_5} = {Q_6} = Q$$
$${R_9} = {R^3} + 3{R^2}Q$$
$${Q_9} = 3R{Q^2} + {Q^3}$$
و در صورتی که:
$${R_4} \ne {R_5} \ne {R_6}$$
$${Q_4} \ne {Q_5} \ne {Q_6}$$
$${R_9} = {R_4}{R_5}{R_6} + {R_4}{R_5}{Q_6} + {R_5}{R_6}{Q_4} + {R_6}{R_4}{Q_5}$$
$${Q_9} = {R_4}{Q_5}{Q_6} + {R_5}{Q_6}{Q_4} + {R_6}{Q_4}{Q_5} + {Q_4}{Q_5}{Q_6}$$
و در حالت خاص این مسئله که قابلیت اطمینان هر یک از عضوها برابر 0.8 است:
$${R_9} = 0.8960$$
$${Q_9} = 0.1040$$
$${Q_{11}} = 0.06237$$
سیستمهای با عضوهای مازاد آماده کار (Standby Redundant System)
مفاهیم مازاد
در سیستم با شبکه موازی علی‌رغم نیاز سیستم به عملکرد فقط یکی از عضوها، همه عضوها در حال کار و فعال می‌باشد. در برخی سیستم‌ها با وجود عضوهای موازی فقط یکی از آن‌ها فعال و سایر عضوها در حالت آماده کار نگهداشته می‌شود و فقط وقتی فعال می‌شود که عضو در حال کار از کار بیفتد.
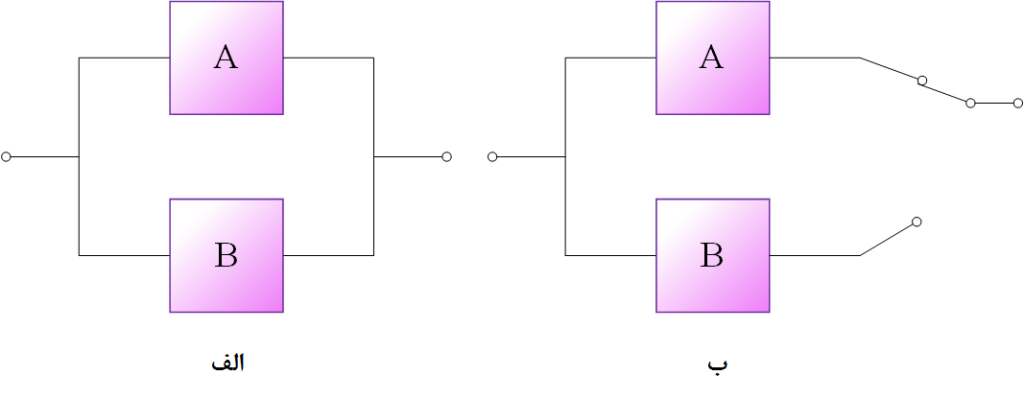
وضعیت‌دهی بی‌نقص (Perfect Switching)
وضعیت‌دهی بی‌نقص، به مفهوم عملکرد صحیح و کامل در شرایط کار سیستم و همچنین به هنگام وضعیت‌دهی در صورت از کار افتادن عضو در حال کار می‌باشد.
با فرض این که عضو $B$ در وضعیت انتظار دچار از کار افتادگی نمی‌شود و از کار افتادن آن مستلزم کاربری آن و از کار افتادن عضو $A$ باشد چنین خواهد شد که از کار افتادن سیستم در اثر از کار افتادن عضو $B$ اتفاق می‌افتد مشروط بر آن که عضو $A$ از کار افتاده باشد. نمایش ریاضی به صورت در پی آمده خواهد شد:
$${Q_{sys}} = {Q_A}\;.\;Q(B|\bar A)$$
و در صورتی که عضوهای و مستقل باشد:
رابطه (11)
$${Q_{sys}} = {Q_A}\;.\;{Q_B}$$
وضعیت‌دهی با احتمال وقوع نقص (Imperfect Switching)
در وضعیت‌دهی از عضو $A$ به عضو $B$ به هنگام از کار افتادن عضو $A$ ممکن است وضعیت دهنده (سوئیچ) دچار نقص شود. با نشان دادن احتمال عملکرد صحیح وضعیت دهنده با ${P_s}$، احتمال عمل نکردن آن \[{\bar P_s} = 1 – {P_s}\] خواهد شد و مسئله در این حالت بر مبنای روش احتمالات شرطی حل می‌شود:
$$\begin{array}{l}
P(system\,Failure)\\
= P(system\,Failure\,|\\
\,\,\,\,successful\,changeover) \times {P_s}\\
+ P(system\,Failure\,|\\
\,\,\,\,unsuccessful\,changeover) \times {{\bar P}_s}
\end{array}$$
بنابراین:
رابطه (12)
$$\begin{array}{l}
{Q_{sys}} = {Q_A}{Q_B}{P_s} + {Q_A}\;.\;{{\bar P}_s}\\
\;\;\;\;\;\; = {Q_A}{Q_B}{P_s} + {Q_A}(1 - {P_s})\\
\;\;\;\;\;\; = {Q_A}{Q_B}{P_s} + {Q_A} - {Q_A}{P_s}\\
\;\;\;\;\;\; = {Q_A} - {Q_A}{P_s}(1 - {Q_B})
\end{array}$$
حال با توجه به این که در حین عملکرد عضوهای $A$ و یا $B$ احتمال وقوع نقص در عملکرد وضعیت دهنده وجود دارد، وضعیت دهنده را باید به عنوان یکی از عضوهای سیستم با قابلیت اطمینان مربوطه‌اش در مدلسازی شبکه مطابق شکل (10) در نظر گرفت.
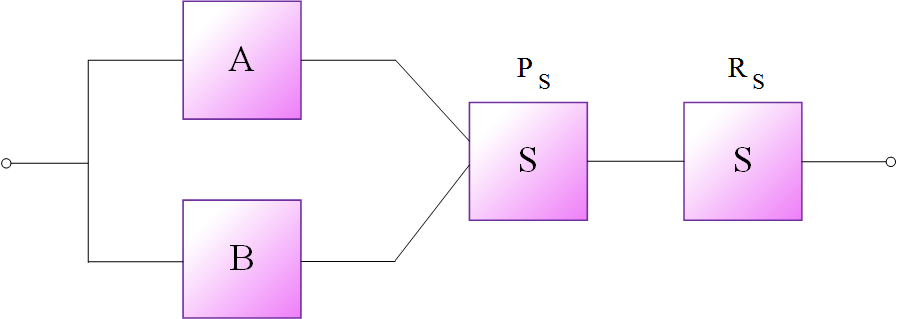
در این شکل احتمال وضعیت‌دهی صحیح ${P_s}$ و قابلیت اطمینان وضعیت دهنده برای تداوم کار ${R_s}$، جداگانه منظور می‌شود. ${P_s}$ در محاسبه قابلیت اطمینان انشعاب‌های آماده کار و ${R_s}$ به عنوان عضو دیگری به صورت متوالی با آن‌ها به کار می‌رود.
رابطه (13)
$$\begin{array}{l}
{Q_{sys}} = [{Q_A} - {Q_A}{P_s}(1 - {Q_B})]\\
\,\,\,\,\,\,\,\,\, + {Q_s} - [{Q_A} - {Q_A}{P_s}(1 - {Q_B})]{Q_s}
\end{array}$$
رابطه (14)
$${R_{sys}} = {R_s}[1 - ({Q_A} - {Q_A}{P_s}(1 - {Q_B}))]$$
مثال (10): مطلوب است تعیین قابلیت اطمینان سیستمی مطابق شکل (9) بر مبنای قابلیت اطمینان 0.9، 0.96 به ترتیب برای عضوهای $A$ و $B$ در صورتی که
الف) وضعیت دهنده بی‌نقص عمل کند.
ب) احتمال وقوع نقص در وضعیت دهنده برابر 0.08 به هنگام وضعیت‌دهی
ج) علاوه بر شرایط «ب» قابلیت اطمینان وضعیت دهنده به هنگام کار برابر 0.98 باشد.
الف)
$$R = 1 - 0.1 \times 0.04 = 0.996$$
ب)
$$R = 1 - (0.1 \times 0.1 \times 0.92(1 - 0.04)) = 0.988$$
ج)
$$R = 0.98 \times 0.988 = 0.969$$
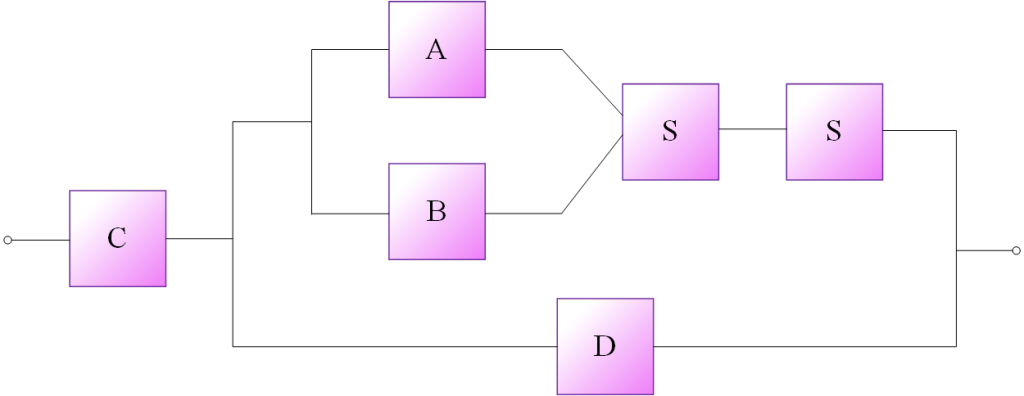
مثال (11): مطابق شکل (11) سیستمی با وجود شرایط قسمت ج در مثال (10) موازی با عضو $D$ و مجموعاً به صورت متوالی با عضو $C$ در اختیارست. مطلوب است تعیین قابلیت اطمینان سیستم مشروط بر آن که قابلیت اطمینان عضوهای $D$ و $C$ به ترتیب 0.8 و 0.99 باشد.
$$\begin{array}{l}
{R_{sys}} = {R_C}(1 - {Q_D}(1 - 0.969))\\
\;\;\;\;\; = 0.99(1 - 0.2(1 - 0.969)) = 0.984
\end{array}$$