مبانی تئوری احتمالات
تعداد بازدید: 2633
زمان مطالعه: 16 دقیقه
فهرست مطالب این نوشته
مفاهیم احتمال
کلمه احتمال در زندگی روزمره به صورت مکرر به معنای شانس وقوع رخدادها به کار می‌رود. احتمال از نظر ریاضی، شاخصی است عددی که مقدار آن می‌تواند از صفر تا یک باشد (شکل 1). وقتی احتمال برابر صفر است مبیّن وقوع غیرممکن مطلق یا به عبارتی عدم وقوع قطعی است و زمانی که برابر یک است مبیّن وقوع قطعی و یا یقین مطلق است. از نظر فلسفی ممکن است ادعا شود که هرگز حدود پایینی و بالایی احتمال حاصل نمی‌شود ولی از نظر مهندسی با دیدگاه واقع‌گرایانه چنین امری می‌تواند محقق شود. به عنوان مثال احتمال اینکه شخصی برای ابد زنده بماند برابر صفر است و احتمال اینکه بالأخره روزی می‌میرد برابر یک است.
رابطه (1) نیز احتمال موفقیت و شکست را نشان می‌دهد:
رابطه (1)
$$\begin{array}{l}
P(success) = \frac{{number\,of\,successes}}{{number\,of\,possible\,\,outcomes}}\\
= \frac{s}{{s + f}} = p
\end{array}$$
$$\begin{array}{l}
P(failure) = \frac{{number\,of\,failures}}{{number\,of\,possible\,\,outcomes}}\\
= \frac{f}{{s + f}} = q
\end{array}$$
که در آن $s$ تعداد حالاتی است که منجر به موفقیت می شود و $f$ تعداد حالاتی است که منجر به عدم موفقیت می شود. لذا: $p + q = 1$
مثال (1): یک سکه و احتمال شیر و خط را برای آن در نظر بگیرید. در هر بار چرخش سکه $s = f = 1$ و لذا احتمال شیر و یا خط هر کدام برابر $\frac{1}{{1 + 1}}$ میباشد.
مثال (2): یک طاس و احتمال نتیجه وجه شماره 4 در هر انداختن آن را در نظر بگیرید. هرگاه به حصول وجه شماره 4 موفقیت اطلاق شود، با توجه به شش وجه از مکعب طاس $s = 1$ و $f = 5$ نمایانگر آن است که به پنج طریق، وجه شماره 4 حاصل نمی‌شود. بنابراین احتمال وقوع این وجه برابر $\frac{1}{{5 + 1}}$ و احتمال اینکه این وجه حاصل نشود برابر $\frac{5}{6}$ میباشد.
نمودارهای وِن (Venn Diagrams)
در ارزیابی قابلیت اطمینان سیستم‌ها و در پیش‌بینی احتمال رفتار کلی آن‌ها به ترکیب احتمال حادثه‌های منفرد نیاز داریم. تعدادی قواعد احتمال امکان این کار را فراهم می‌سازد که در ادامه مطرح می‌کنیم.
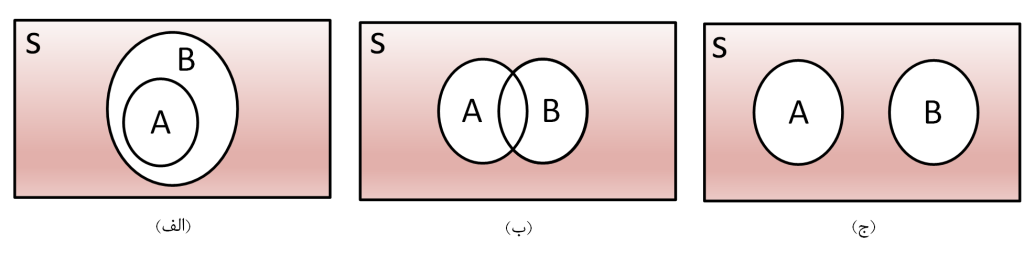
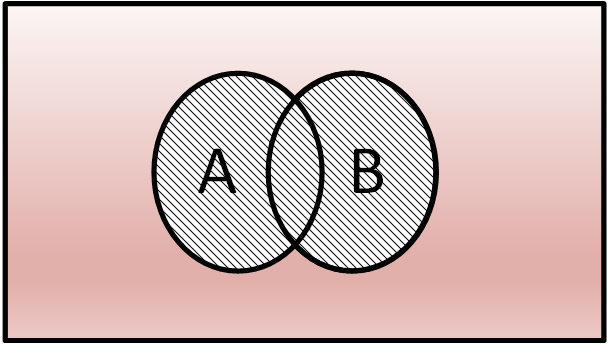
احتمال وقوع دو حادثه و یا بیشتر در این فضا در تلفیق با هم مورد بررسی قرار می‌گیرد. در اینجا دو حادثه $A$ و $B$ را مطابق با شکل (2) در نظر بگیرید. هرگاه وقوع حادثه $A$ کلاً توسط وقوع حادثه $B$ احاطه شده باشد (شکل (2) – الف) در این صورت حادثه $A$ زیرمجموعه ای از حادثه $B$ است. این یکی از حالات است و به طور کلی ممکن است $A$ و $B$ در بخش محدودی همپوشانی داشته (شکل (2) – ب) و یا به‌هیچ‌وجه قسمت مشترک نداشته باشند (شکل (2) – ج).
قواعد تلفیق احتمالات (Rules for Combining Probabilities)
قاعده 1: حادثه‌های مستقل (Independent Events)
دو حادثه وقتی مستقل است که وقوع هر یک هیچ تأثیری در احتمال وقوع دیگری نداشته باشد.
مثال (3): پرتاب یک تاس و چرخش سکه حادثه‌های مستقل است زیرا اینکه کدام روی سکه نتیجه شود هیچ تأثیری در نتیجه تاس نخواهد داشت.
قاعده 2: حادثه‌های دو به دو ناسازگار (Mutually Exclusive Events)
دو حادثه دو به دو ناسازگار است وقتی که هرگز به طور همزمان نتواند واقع شود. این حالت را می‌توان با نمودار ون مطابق شکل (2) – ج نمایش داد که در آن وقوع حادثه‌های $A$ و $B$ هیچ ناحیه مشترکی ندارند. به نحوی که وقتی حادثه $A$ اتفاق افتد حادثه $B$ قطعاً واقع نخواهد شد.
مثال (4): وقتی یک تاس انداخته می‌شود وقوع وجوه شماره 1 تا 6 حادثه‌هایی دو به دو ناسازگار است، زیرا که هرگز به طور همزمان نمی‌تواند واقع شود. همچنین به همین دلیل موفقیت و شکست در عملکرد یک وسیله، حادثه‌های دو به دو ناسازگار میباشد.
قاعده 3: حادثه‌های مکمل (Complementary Events)
دو نتیجه وقوع و عدم وقوع حادثه‌های مکمل‌اند، زیرا در صورت عدم وقوع یکی، دیگری وقوع می‌یابد. نمایش این حالت با استفاده از نمودار ون شکل (3) میسر است. در صورتی که احتمال وقوع حادثه‌های $A$ و $B$ را با $P(A)$ و $P(B)$ نمایش دهیم داریم:
رابطه (2)
$P(A) + P(B) = 1$ یا $P(B) = P(\bar A)$
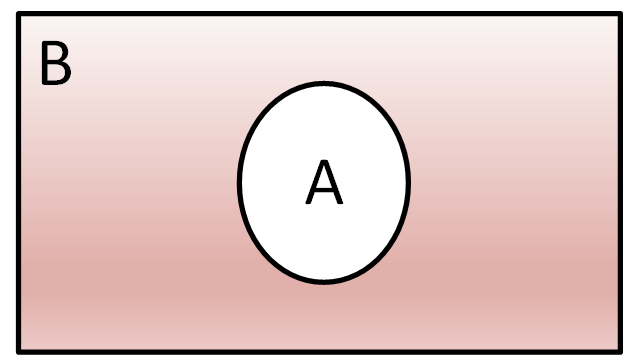
که در آن $P(\bar A)$ احتمال عدم وقوع حادثه $A$ است.
مثال (5): در مثال چرخش سکه، نتایج شیر “H” و خط “T” حادثه‌های مکمل می‌باشند:
$P(H) + P(T) = 1$ یا $P(H) = P(\bar T)$
همچنین وقتی برای عملکرد یک وسیله دو حالت موفقیت و شکست قائل باشیم، این دو حالت حادثه‌های مکمل خواهند بود. همچنین نتیجه می‌شود که دو حادثه مکمل دو به دو ناسازگار است، ولی بدیهی است که عکس آن صادق نیست و الزاماً دو حادثه ناسازگار مکمل نیستند.
قاعده 4: حادثه‌های شرطی (Conditional Events)
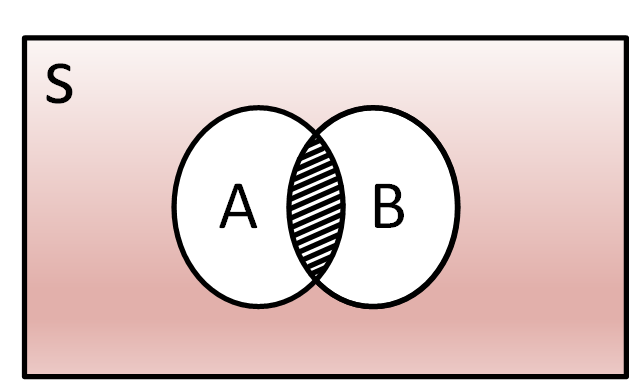
وقوع حادثه‌های شرطی به یکدیگر وابسته باشد؛ برای دو حادثه شرطی، احتمال وقوع حادثه $A$ وقتی حادثه $B$ واقع شده باشد مطرح می‌شود و نمایش ریاضی آن به شکل $P(A|B)$ خواهد بود که در آن خط عمودی حائل به مفهوم «وقتی واقع شده باشد» است. این حالت به نام احتمال شرطی و با استفاده از نمودار ون به شکل (4) نمایش‌پذیر است.
رابطه (3)
\[P(A|B) = \frac{{number\,of\,ways\,A\,\& \,B\,can\,occur}}{{number\,of\,ways\,B\,can\,occure}}\]
معادله فوق نشان دهنده نسبت تعداد دفعاتی است که در ضمنِ وقوع حادثه $B$، حادثه $A$ می‌تواند واقع شود به تعداد دفعاتی که حادثه $B$ می‌تواند واقع شود. وقوع همزمان $A$ و $B$ در نمودار هاشور زده شده است و آن را به طریق ریاضی با $(A \cap B)$ به معنای اشتراک نشان می‌دهند و احتمال وقوع آن عبارت است از:
رابطه (4)
$$P(A \cap B) = \frac{{A \cap B}}{S}$$
متناظراً: $P(B) = \frac{B}{S}$ بنابراین:
رابطه (5)
$$P(A|B) = \frac{{A \cap B}}{B} = \frac{{S.P(A \cap B)}}{{S.P(B)}} = \frac{{P(A \cap B)}}{{P(B)}}$$
متشابهاً: $P(B|A) = \frac{{P(A \cap B)}}{{P(A)}}$
قاعده 5: وقوع همزمان حادثه‌ها (Simultaneous Occurrence)
وقوع همزمان دو حادثه $A$ و $B$ عبارت از وقوع هر دو حادثه $A$ و $B$ با هم و در قالب نمودار ون مطابق شکل (4) به صورت قسمت هاشور خورده و به صورت ریاضی به شکل‌های $(AB)$ یا $B)$ و $(A$ و $(A \cap B)$ نمایش می‌یابد. رخدادهای $A$ و $B$ به ترتیب زیر دو حالت مستقل و غیرمستقل برایشان مطرح است:
الف) حادثه‌های مستقل: در این صورت وقوع هر یک هیچ‌گونه تأثیری در احتمال وقوع دیگری نخواهد داشت:
رابطه (6)
$P(A|B) = P(A)$ یا $P(B|A) = P(B)$
$P(A \cap B) = P(A)P(B)$
همچنین معادله اخیر نشان دهنده روش تعیین احتمالات تلفیقی است و هرگاه $n$ حادثه مستقل مطرح باشد خواهیم داشت:
رابطه (7)
$$P({A_1} \cap {A_2}... \cap {A_i} \cap ... \cap {A_n}) = \prod\limits_{i = 1}^n {P({A_i})} $$
مثال (6): دو قطعه $A$ و $B$ انتخاب شده است. احتمال اینکه قطعه $A$ سالم باشد 0.9 است و احتمال سالم بودن قطعه $B$ برابر 0.95 میباشد. احتمال اینکه هر دو قطعه سالم باشد:
$$\begin{array}{l}
P({A_G} \cap {B_G}) = P(A\;true).P(B\;true)\\
= 0/9 \times 0/95 = 0/855
\end{array}$$
ب) حادثه‌های وابسته: هرگاه دو حادثه مستقل نباشد در این صورت احتمال وقوع یک حادثه متأثر از احتمال وقوع حادثه دیگر است، و همچنان می‌توان از معادله احتمال شرطی استفاده کرد ولی مانند قبل نمی‌توان آن را ساده نمود لذا:
رابطه (8)
$$P(A \cap B) = P(B|A).P(A) = P(A|B).P(B)$$
مثال (7): یک کارت از مجموعه یک بسته 52 کارت بازی بیرون کشیده می‌شود. هرگاه کارت قرمز به عنوان حادثه $A$ و کارت تصویر صورت به عنوان حادثه $B$ تلقی شود، احتمال وقوع همزمان حادثه‌های $A$ و $B$ چیست؟
$$P(A) = \frac{{26}}{{52}}$$
و در صورتی که حادثه واقع شده باشد فضای وقوع حادثه شامل 26 طریق می‌شود که تنها 6 طریق آن نتیجه کارت تصویر صورت است، بنابراین:
$$P(B|A) = \frac{6}{{26}}$$
$$P(A \cap B) = \frac{6}{{26}} \times \frac{{26}}{{52}} = \frac{6}{{52}}$$
همچنین به طریقی دیگر:
$$P(B) = \frac{{12}}{{52}}$$
$$P(A|B) = \frac{6}{{12}}$$
$$P(A \cap B) = \frac{6}{{12}} \times \frac{{12}}{{52}} = \frac{6}{{52}}$$
این دو شیوه هر دو دارای اهمیت اساسی است و کاربرد متداولی دارد.
قاعده 6: وقوع حداقل یکی از دو حادثه (Occurrence of at least one of two Event)
وقوع حداقل یکی از دو حادثه $A$ و $B$، عبارت از وقوع $A$ یا وقوع $B$ و یا وقوع هر دو که با استفاده از نمودار ون به شکل (5) محدوده وقوع را می‌توان با هاشور نشان داد و به صورت نمایش ریاضی خواهیم داشت:
رابطه (9)
$(A \cup B)\,(A\,\,\,or\,\,\,B)$ یا $(A + B)$
در این شرایط سه حالت مختلف پیش می‌آید:
- حادثه‌ها مستقل هستند ولی ناسازگار نیستند.
- حادثه‌ها مستقل و در عین حال ناسازگار هستند.
- حادثه‌ها مستقل نیستند.
الف) حادثه‌های مستقل و غیرناسازگار: به دو روش تحلیلی و کاربرد نمودار ون می‌توان این حالت را بررسی کرد.
روش تحلیلی
رابطه (10)
$$\begin{array}{l}
P(A \cup B) = P(A\,\,or\,\,B\,\,or\,\,both\,\,A\,\,and\,B)\\
= 1 - P(not\,A\,\,and\,\,not\,B)\\
= 1 - P(\bar A \cap \bar B) = 1 - P(\bar A).P(\bar B)\\
= 1 - (1 - P(A))(1 - P(B))\\
= P(A) + P(B) - P(A).P(B)
\end{array}$$
مثال (8): با مرور مثال (6) احتمال اینکه حداقل یکی از دو قطعه $A$ یا $B$ سالم باشد خواهد شد:
$$\begin{array}{l}
P(A\;true \cup B\;true)\\
= P(A\;true) + P(B\;true) - P(A\;true)P(B\;true)\\
= 0.9 + 0.95 - 0.9 \times 0.95 = 0.995
\end{array}$$
ب) حادثه‌های مستقل و دو به دو ناسازگار: وقتی که دو حادثه $A$ و $B$ دو به دو ناسازگار است احتمال همزمانی وقوع $P(A).P(B)$ برابر صفر می‌شود و لذا:
رابطه (11)
$$P(A \cup B) = P(A) + P(B)$$
با استفاده از نمودار ون مطابق شکل (2) – ج حالتی مطرح است که حادثه‌های $A$ و $B$ ناحیه مشترکی ندارد و مساحت ناحیه مشترک برابر صفر است.
رابطه (12)
$$P(A \cup B) = P(A) + P(B)$$
و در صورتی که $n$ حادثه مستقل و دو به دو ناسازگار مطرح باشند خواهیم داشت:
رابطه (13)
$$P({A_1} \cup {A_2} \cup ... \cup {A_i} \cup ... \cup {A_n}) = \sum\limits_{i = 1}^n {P({A_i})} $$
مثال (9): احتمال اینکه در هر بار ریختن دو تاس جمع عددی 9 به دست بیاید، چهار حالت خواهد داشت، که این حالت‌ها دو به دو ناسازگار هستند و چون احتمال وقوع هر یک از این چهار حادثه $\frac{1}{{36}}$ است:
$$P(9) = \frac{1}{{36}} + \frac{1}{{36}} + \frac{1}{{36}} + \frac{1}{{36}} = \frac{4}{{36}} = \frac{1}{9}$$
ج) حادثه‌های غیرمستقل: برای این حالت داریم:
رابطه (14)
$$P(A \cup B) = P(A) + P(B) - P(B|A).P(A)$$
$$ = P(A) + P(B) - P(A|B)P(B)$$
مثال (10): در مروری بر مثال (7) برای برآورد احتمال بیرون آوردن کارت قرمز یا صورتی و یا هر دو خواهیم داشت:
احتمال کارت قرمز
$$P(A) = \frac{{26}}{{52}}$$
احتمال کارت صورتی
$$P(B) = \frac{{12}}{{52}}$$
مانند قبل:
$$P(A|B) = \frac{6}{{12}}\,\,\,\,\,\,,\,\,\,\,\,\,P(B|A) = \frac{6}{{26}}$$
بنابراین:
$$P(A|B) = (\frac{{26}}{{52}} + \frac{{12}}{{52}}) - (\frac{6}{{26}} \times \frac{{26}}{{52}}) = \frac{{32}}{{52}}$$
و یا:
$$(\frac{{26}}{{52}} + \frac{{12}}{{52}}) - (\frac{6}{{12}} \times \frac{{12}}{{52}}) = \frac{{32}}{{52}}$$
قاعده 7: کاربرد احتمال شرطی (Application of Conditional Probability)
مفهوم احتمال شرطی در قاعده شماره 4 بیان شد. در اینجا در گسترش این مفهوم وقتی وقوع حادثه $A$ بستگی به وقوع تعدادی حادثه‌های دو به دو ناسازگار ${B_i}$ داشته باشد مورد بررسی قرار می‌گیرد. از معادله (5) داریم:
رابطه (15)
$$P(A \cap B) = P(A|B).P(B)$$
از معادله بالا برای هر یک از حادثه‌های ${B_i}$ داریم:
رابطه (16)
$$\begin{array}{l}
P(A \cap {B_1}) = P(A|{B_1}).P({B_1})\\
P(A \cap {B_2}) = P(A|{B_2})P({B_2})\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots \\
P(A \cap {B_n}) = P(A|{B_n})P({B_n})
\end{array}$$
و لذا:
رابطه (17)
$$\sum\limits_{i = 1}^n {P(A \cap {B_i}) = \sum\limits_{i = 1}^n {P(A|{B_i})P({B_i})} } $$
تحت شرایطی که $i = 4$ و کل نمودار ون برای آن مطابق شکل (6) باشد داریم:
رابطه (18)
$$\sum\limits_{i = 1}^n {P(A \cap {B_i}} ) = P(A)$$
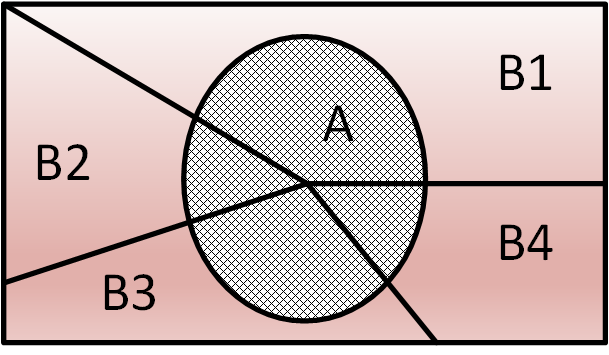
که موجب خلاصه شدن معادله (17) به معادله احتمال شرطی ذیل می‌شود.
رابطه (19)
$$P(A) = \sum\limits_{i = 1}^n {P(A|{B_i}).P({B_i})} $$
این معادله کاربردهای زیادی در ارزیابی قابلیت اطمینان دارد. کاربرد این معادله به ویژه از طریق مثال به نحو بهتری درک می‌شود. هرگاه وقوع حادثه $A$ بستگی به دو حادثه دو به دو ناسازگار و مکمل برای محصول $B$ مطرح باشد (مانند سالم در مقابل معیوب) که به صورت ${B_s}$ و ${B_f}$ نمایش داده شود خواهیم داشت:
رابطه (20)
$$P(A) = P(A|{B_s}).P({B_s}) + P(A|{B_f}).P({B_f})$$
هدف در ارزیابی قابلیت اطمینان، معمولاً تعیین احتمال شکست و یا موفقیت است از این رو معادله بالا به شکل زیر مطرح می‌شود:
احتمال شکست سیستم عبارت است از احتمال شکست سیستم در صورت خوب بودن B ضرب در احتمال سالم بودن B + احتمال شکست سیستم در صورت بد بودن B ضرب دراحتمال بد بودن B.
و در صورتی که در معادله بالا $A$ به عنوان موفقیت سیستم تعریف شود:
احتمال موفقیت سیستم عبارت است از احتمال موفقیت سیستم در صورت خوب بودن B ضرب در احتمال سالم بودن B + احتمال موفقیت سیستم در صورت بد بودن B ضرب دراحتمال بد بودن B.
این دو شکل از تعریف کاربردهای وسیع و مفیدی در ارزیابی قابلیت اطمینان دارند.
مثال (11): سیستمی متشکل از دو عضو $A$ و $B$ است و فقط در صورتی که هر دو عضو $A$ و $B$ از کار بیفتد سیستم از کار خواهد افتاد. احتمال از کار افتادن سیستم چقدر است؟
در صورتی که ${Q_A}$ و ${Q_B}$ نمایانگر احتمال از کار افتادن دو عضو باشد خواهیم داشت:
$$P(failure) = 0 \times (1 - {Q_B}) + {Q_A}.{Q_B} = {Q_A}{Q_B}$$
توزیع‌های احتمال (Probability Distributions)
متغیرهای اتفاقی (Random Variables)
به منظور امکان‌پذیری کاربرد تئوری احتمال برای پیش‌بینی وقوع حادثه‌ها، ضرورتاً باید وقوع آن‌ها کاملاً تصادفی باشد و آن به معنای اتفاقی بودن در میدان‌های زمان و فضا و یا هر دو میباشد. بنابراین پارامترهای حادثه‌ها مانند آهنگ ازکارافتادگی عضوها، مدت انجام تعمیر، مقدار مقاومت الکتریکی و یا مقاومت مکانیکی به عنوان متغیرهای اتفاقی در میدان‌های زمان و فضا مطرح است. این متغیرها ممکن است پیوسته و یا ناپیوسته باشند. نوع ناپیوسته مشخصاً مبیّن تعداد و نمایانگر متغیر شمارش‌پذیر است، مانند یک سکه که دو حالت ناپیوسته دارد. نوع پیوسته مشخصاً مبیّن تعداد نامحدود از مقادیر است و البته این به مفهوم گسترش از $ – \infty $ تا $ + \infty $ برای مقادیر متغیر نیست، بلکه صرفاً بی‌نهایت حالت محتمل را برای آن، مورد نظر قرار می‌دهد. برای مثال شدت جریان الکتریکی از 5 تا 10 آمپر یک متغیر پیوسته با یک چنین ویژگی میباشد.
تابع‌های چگالی و توزیع (Density & Distribution Functions)
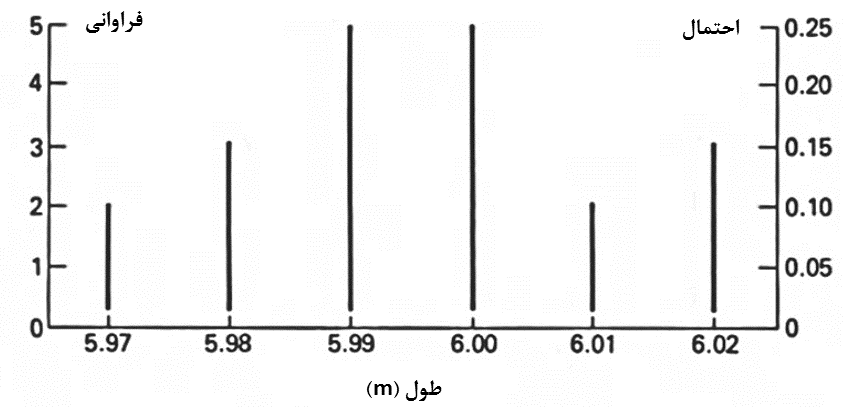
مثال (12): پروفیل‌های اکسترود شده توسط یک ماشین برش در طول‌های 6 متری بریده می‌شود. با یک نمونه‌برداری اتفاقی به تعداد 20 عدد پروفیل بریده شده، طول آن‌ها اندازه‌گیری شده است و نتایج زیر حاصل میباشد.
$$\begin{array}{l}
\underbrace {5.97,\;5.97}_2,\underbrace {5.98,5.98,5.98}_3\\
\underbrace {5.99,\;5.99,\;5.99,\;5.99,5.99}_5\\
\underbrace {6.0,\,6.0,\,6/0,\,6.0,\,6/0}_5,\,\underbrace {6.01,\;6.01}_2\\
\underbrace {6.02,\,6.02,\,6.02}_3
\end{array}$$
این نتایج عددی را می‌توان به روش ترسیمی به صورت توزیع فراوانی مطابق شکل (7) نشان داد. منظور از فراوانی همان تعداد دفعاتی است که نتیجه مشخصی برای طول بریده شده به دست آمده است.
روش ترسیمی دیگر، برای ارائه اطلاعات، گروه‌بندی طول‌های نزدیک به هم مطابق با شکل (8) میباشد. این روش به ویژه وقتی حجم اطلاعات زیاد باشد کار را ساده می‌کند و با سهولت بیشتری می‌توان نتایج را تفسیر کرد.
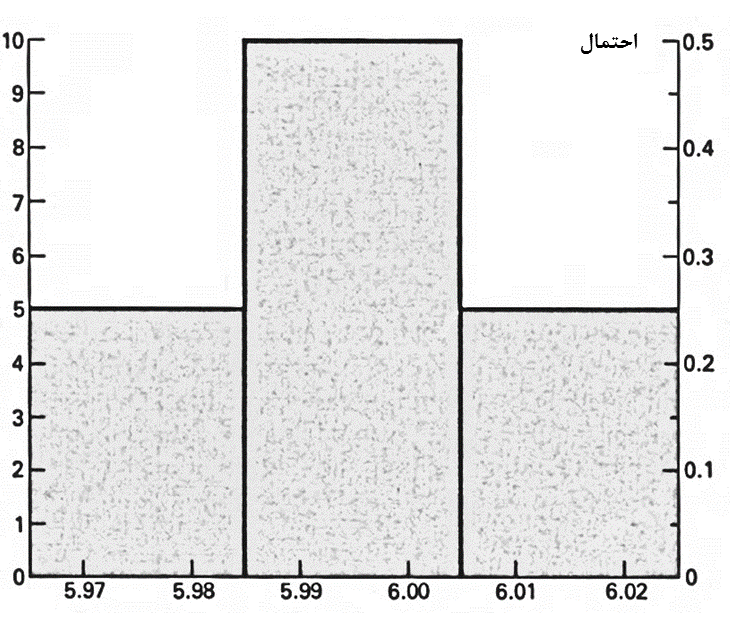
----------------شکل 8: توزیع‌های فراوانی احتمال – اطلاعات گروهی
در شکل‌های (7) و (8) محور عرض‌ها برحسب این مقادیر یعنی مقادیر احتمال نیز مدرّج شده است. وقتی روش مدرّج کردن بر مبنای احتمال صورت گیرد تابع احتمال حاصل می‌شود. و از آنجایی که همه نتایج فضای نمونه منظور می‌شود جمع احتمالات باید برابر واحد شود:
رابطه (21)
$$\sum\limits_{i = 1}^n {P({x_i}) = 1} $$
که در آن ${x_i}$ نمایانگر نتیجه $i$ اُم و یا در این مثال طول $i$ اُم است. روش دیگری در نشان دادن همین مجموعه اطلاعات مورد استفاده است و آن کاربرد تابع توزیع احتمال است که فراوانی نسبی تجمعی در آن مورد ملاحظه قرار می‌گیرد. بدین ترتیب که نتایج نامرتب به ترتیب صعودی تنظیم می‌شود و احتمال وقوع از کوچکترین مقدار نتیجه متوالیاً جمع می‌شود. بنابراین به ازای هر نتیجه مشخص، احتمال وقوع کلیه نتایج محدود به آن نتیجه تعیین خواهد شد. این روش در شکل‌های (9) الف و ب برای اطلاعات مثالِ مورد بحث ارائه شده است. از آنجایی که همه نتایج میسّر در فضای نمونه در نظر گرفته می‌شود، بنابراین نهایتاً فراوانی نسبی تجمعی به عدد 1.0 خواهد رسید که به مفهوم وقوع قطعی طول‌ها محدود به حد بالایی میباشد.
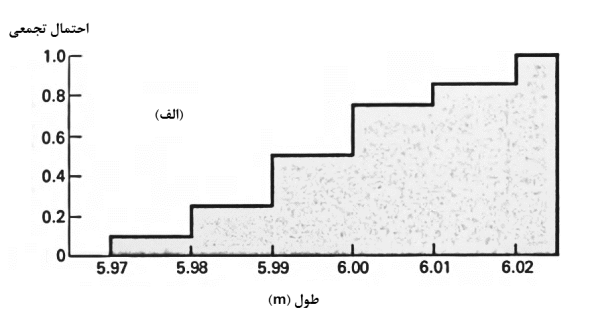
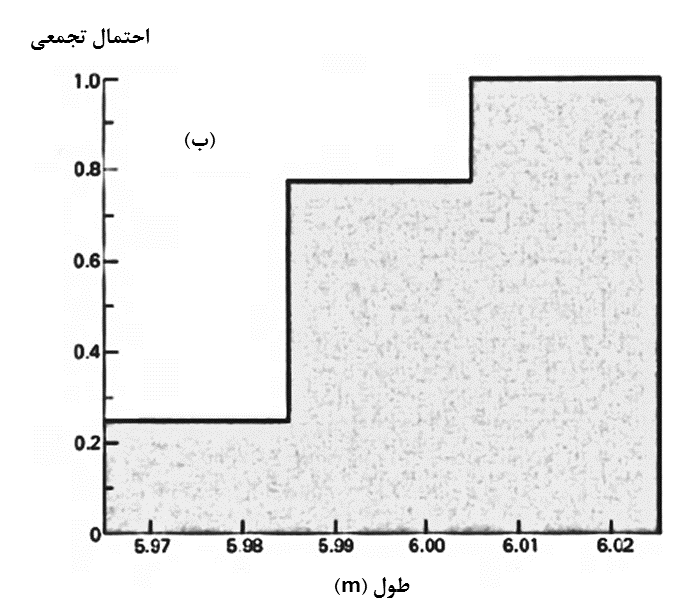
شکل 9: تابع‌های توزیع احتمال الف- اطلاعات تفکیکی ب- اطلاعات گروهی
شکل (10) نیز حالت پیوسته را نشان می‌دهد.
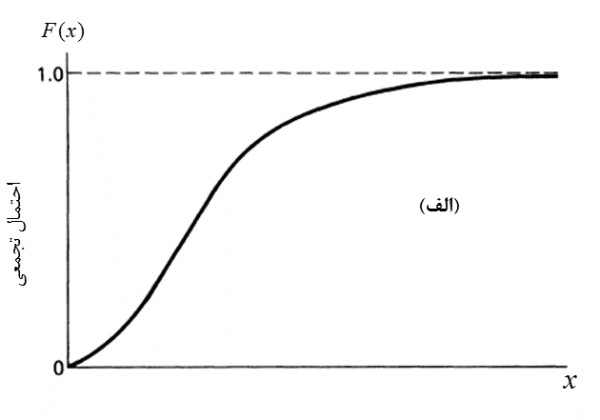
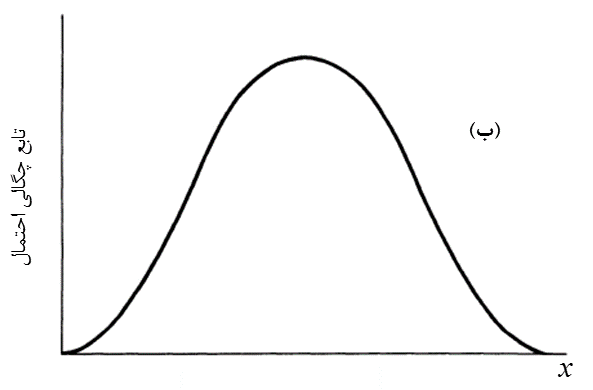
شکل 10: متغیر اتفاقی پیوسته الف- احتمال تجمعی ب- تابع چگالی احتمال
همان‌گونه که برای یک متغیر ناپیوسته تابع توزیع احتمال با جمع زدن مقادیر تابع چگالی احتمال به دست آمد، برای یک متغیر پیوسته، تابع توزیع احتمال با انتگرالگیری تابع چگالی احتمال به دست می‌آید، لذا با مشتق‌گیری از تابع توزیع احتمال می‌توان تابع چگالی احتمال را به دست آورد:
رابطه (22)
$$f(x) = \frac{{dF(x)}}{{dx}}$$
و یا:
رابطه (23)
$$F({x_1}) = \int_{ - \infty }^{{x_1}} {f(x)dx} $$
معادله اخیر معادل جمع زدن دفعات وقوع برای یک متغیر ناپیوسته است و احتمال وقوع محدود به مقدار $x{}_1$ را به دست می‌دهد. همچنین از این معادله در تعیین احتمال وقوع محدود به هر حدود پایینی و بالایی دلخواه استفاده می‌شود یعنی:
رابطه (24)
$$P(a \le x \le b) = \int_a^b {f(x)dx} $$
امید ریاضی یا مقدار انتظاری (Mathematical Expectation)
توصیف رفتار اتفاقی یک سیستم و یا مجموعه اطلاعات و نتایج، توسط چند پارامتر مشخص، کاربردی‌تر از توصیف ترسیمی است. این امر به ویژه در محاسبات و ارزیابی‌ها مانند ارزیابی قابلیت اطمینان سیستم‌ها به وضوح مشخص است. روش توصیف پارامتریک با کاربرد اعدادی که در ریاضی به اصطلاح ممان‌های توزیع نامیده می‌شود صورت می‌گیرد. مهم‌ترین این ممان‌ها مقدار انتظاری است که اصطلاحاً مقدار میانگین و یا میانگین جامعه نیز نامیده می‌شود. در ریاضیات این اولین ممان یک توزیع است. همه افراد با روش محاسبه مقدار میانگین آشنا هستند و آن عبارت از تعیین حاصل تقسیم مجموع نتایج به تعداد آن میباشد. با کاربرد اطلاعات مثال طول پروفیل‌های بریده شده خواهیم داشت:
$$\frac{1}{{20}}(\underbrace {5.97 + 5.97}_2 + 5.98 + ... + 6.02) = 5.9955$$
این نتیجه با اعمال ضریب وزنی، بر مبنای فراوانی نسبی هر یک از طول‌ها نیز تعیین‌پذیر است:
$$\begin{array}{l}
\frac{2}{{20}} \times 5.97 + \frac{3}{{20}} \times 5.98 + \frac{5}{{20}} \times 5.99\\
+ \frac{5}{{20}} \times 6.00 + \frac{2}{{20}} \times 6.01 + \frac{3}{{20}} \times 6.02 = 5.9955
\end{array}$$
و از آنجایی که فراوانی نسبی وقوع، همان احتمال وقوع است لذا در تعیین مقدار انتظاری $E(x)$ برای $n$ نتیجه ${x_i}$ با احتمال وقوع ${p_i}$ برای هر یک از نتایج خواهیم داشت:
رابطه (25)
$$E(x) = \sum\limits_{i = 1}^n {{x_i}{p_i}\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{p_i} = 1} } $$
و برای هنگامی که متغیر مورد نظر پیوسته باشد با انتگرالگیری به جای تعیین مجموع، معادله فوق به صورت در پی آمده در می‌آید:
رابطه (26)
$$E(x) = \int_{ - \infty }^\infty {xf(x)dx} $$
توجه شود که $\int_{ – \infty }^\infty {f(x)dx} = 1$
مثال (13): در تکرار انداختن تاس به دفعات بسیار زیاد مقدار انتظاری برای نتایج چه عددی است؟
$$\begin{array}{l}
E = \frac{1}{6} \times 1 + \frac{1}{6} \times 2 + \frac{1}{6}\\
\times 3 + \frac{1}{6} \times 4 + \frac{1}{6} \times 5 + \frac{1}{6} \times 6 = 3.5
\end{array}$$
پراکنش و انحراف استاندارد (Variance and Standard Deviation)
پراکنش نتایج توسط ممان مرکزی دوم توزیع فراوانی به نام واریانس اندازه‌گیری می‌شود. ممان مرکزی kاُم برای یک توزیع فراوانی با عبارت زیر تعریف می‌شود:
رابطه (27)
$${M_k} = E{(x - E(x))^k}$$
و بنابراین برای واریانس داریم:
رابطه (28)
$$\begin{array}{l}
V(x) = E{[x - E(x)]^2}\\
= E[{x^2} - 2xE(x) + {E^2}(x)]\\
= E({x^2}) - E(2xE(x)) + E[{E^2}(x)]\\
= E({x^2}) - 2E(x)E(x) + {E^2}(x)\\
= E({x^2}) - {E^2}(x)
\end{array}$$
ملاحظه می‌شود که در تعیین واریانس نیاز به تعیین مقدار انتظاری از نتایج میباشد و بنابراین معادله تعیین واریانس به شکل اولیه و یا به شکل بسط یافته آن هر دو میسّر است و به صورت‌های زیر نمایش می‌یابند:
رابطه (29)
$$\begin{array}{l}
V(x) = \sum\limits_{i = 1}^n {{{({x_i} - E(x))}^2}{P_i}} \\
V(x) = \sum\limits_{i = 1}^n {(x_i^2{P_i}) - {E^2}(x} )
\end{array}$$
برای تعیین واریانس متغیرهای پیوسته از همین معادلات و با جایگزینی عمل انتگرالگیری به جای تعیین مجموع استفاده می‌شود. واریانس مقداری است که عملاً کاربرد ملموسی نداشته و کمتر مورد استفاده قرار می‌گیرد و در عوض ریشه دوم آن با علامت مثبت به نام انحراف استاندارد مورد استفاده قرار می‌گیرد و آن را با $\sigma $ نمایش می‌دهند.
رابطه (30)
$$\sigma = + \sqrt {V(x)} $$
مثال (14): مطلوب است تعیین واریانس و انحراف استاندارد طول پروفیل‌های بریده شده در مثال (12).
$$\begin{array}{l}
V(x) = {5.97^2} \times \frac{2}{{20}} + {5.98^2} \times \frac{3}{{20}} + {5.99^2} \times \frac{5}{{20}}\\
+ {6.00^2} \times \frac{5}{{20}} + {6.01^2} \times \frac{2}{{20}} + {6.02^2} \times \frac{3}{{20}}\\
- {5.9955^2} = 2.248 \times {10^{ - 4}}\\
\sigma (x) = 1.499 \times {10^{ - 2}}m
\end{array}$$
روش محاسباتی فوق نسبت به روش دیگر ترجیح دارد زیرا در استفاده از معادله (29) وقتی اختلاف نتایج با مقدار انتظاری یا میانگین، کوچک باشد با توان دوم، کوچکتر هم شده و حفظ دقت محاسبات را دشوار می‌کند.