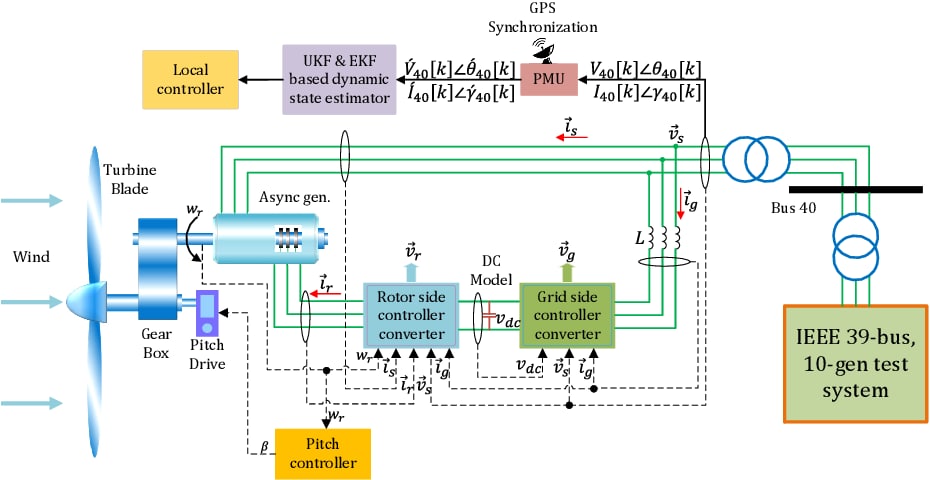
تخمین حالت دینامیک در سيستم‌هاي قدرت
تعداد بازدید: 3783
زمان مطالعه: 13 دقیقه
فهرست مطالب این نوشته
مقدمه
تخمين حالت در سيستم‌هاي قدرت بر دو نوع استاتيكي و ديناميكي می‌باشد. اگر بردار حالت براي يك زمان خاص $t$ از مجموعه اندازه‌گيري‌ها در همان لحظه از زمان به دست آيد، اين روش تخمين را تخمين حالت استاتيكي گويند. براي اينكه بتوان متغيرهاي حالت شبکه قدرت را در زمان‌هاي مختلفي بدست آورد و محاسبه كرد، اين فرآيند محاسبه بردار حالت بايستي در بازه‌هاي زماني مناسب تكرار شود. در شرايط نرمال، شبکه قدرت شبه ايستا است و از اينرو تغييرات آن به كندي اما پايدار و پيوسته مي‌باشد. اين تغييرات در شبکه از تغييرات بارها ناشي مي‌شود و درنتيجه بايد به تناسب تغيير بار، توليد نيز تنظيم گردد و ازاينرو توان‌هاي جاري و تزريقي نيز تغيير مي‌كنند. در نتیجه متغیرهای سيستم قدرت نیز به‌طور ديناميكي تغییر می‌نمایند. در نهايت براي داشتن يك پایش و نظارت پيوسته از شبکه قدرت، تخمين حالت بايد در بازه‌هاي زماني كوچك اجرا شود. اما ازآنجايي كه شبکه با افزودن بارها و ژنراتورها همواره در حالت توسعه است، ابعاد سيستم به شدت بزرگ شده و اجراي تخمين حالت استاتيكي در بازه‌هاي زماني كوتاه، محاسبات سنگيني را در بر خواهد داشت. بنابراين، تخمين حالت استاتيكي که در بازه‌های زمانی در حد دقیقه اجرا می‌گردد نباید به طور مؤثر اين رفتار ديناميكي شبکه قدرت را دنبال كند.
اين موضوع منجر به توسعه الگوريتمي ديگر به نام تخمين حالت ديناميكي (DSE) شده است كه از مدل فيزيكي واقعي متغير با زمان شبکه قدرت استفاده می‌كند. DSE داراي دو مزيت دقت بيشتر و توانايي پيش‌بيني حالت‌هاي سيستم در مرحله بعدي يا زمان بعدي است. به عبارت ديگر، تخمين حالت ديناميكي با دانستن بردار حالت در يك لحظه از زمان $t$ و مدل رياضي سيستم قدرت، بردار حالت سيستم قدرت در زمان بعدي $t + 1$ را پيش‌بيني مي‌كند. اكثر الگوريتم هاي تخمين حالت ديناميكي از مدل رياضي رفتار زماني سيستم براي نشان دادن تغييرات ديناميكي شبکه قدرت استفاده مي‌كنند و حالت سيستم را در مرحله بعد پيش‌بيني مي‌كنند. اين توانايي پيش‌بيني، مزيت‌هاي بسيار مهمي دارد. به عنوان مثال با به کارگیری این نوع تخمین، تحليل امنيت مرحله بعدي قابل اجراست. همچنین اپراتور سيستم زمان بيشتري براي تصميم‌گيري‌های كنترلي مانند پخش‌بار اقتصادي، ارزيابي امنيت و ديگر توابع مرتبط خواهد داشت. ازاينرو تخمين حالت ديناميكي شاخه مهمي در تخمين حالت سيستم‌هاي قدرت مي‌باشد كه پتانسيل بالايي در پایش زمان‌واقعی و كنترل سيستم هاي قدرت دارد. بعضي از مزایای تخمین حالت دینامیکی عبارتند از :
-
اجازه خواهد داد كه تحليل امنيت جلوتر انجام پذيرد و از اين رو اپراتور زمان بيشتري را در طول خطاها داشته باشد.
-
كمك خواهد كرد كه داده‌هاي بد، شناسايي و حذف شوند و از اين رو كارآيي تخمين‌گر بهبود خواهد يافت.
-
در مواردي كه اندازه‌گيري‌‌هاي كاذب استفاده مي‌شوند، تخمين حالت ديناميكي مقادير با كيفيت بالا و خطاي كم را فراهم مي‌نمايد و از اين رو از بروز شرايط بد جلوگيري مي‌شود.
-
تخمين حالت ديناميكي مي‌تواند براي معتبرسازي داده‌ها استفاده شود، ازآنجائیکه حالت‌ها براي نمونه زماني بعد پيش بيني مي‌شوند.
-
همين‌طور، با كمك بردار حالت پيش‌بيني شده، امكان شناسايي خطاهاي ناگهاني، خطاهاي ساختاري و ساير خطاها در سيستم وجود دارد.
اين مزيت‌ها در تخمين حالت ديناميكي سبب شده است كه اين الگوريتم نقش مهمي را در سيستم هاي مديريت انرژي امروزي بازي كند.
تخمین حالت به کمک فیلتر کالمن
در سال 1974، Debs تئوري تخمين حالت ديناميكي برپايه فيلتر كالمن را ارائه كرد. براي بهبود اجراي فيلتركردن، به خصوص در شرايط تغيير ناگهاني بار، روش‌هاي فيلتر كالمن بسط داده شده‌اند. همچنين مي‌توان از تكنيك‌هاي برپايه هوش مصنوعي نظير شبكه‌هاي عصبي و منطق‌فازي براي تخمين حالت ديناميكي استفاده نمود. در تخمين حالت ديناميكي با استقاده از روش فيلتر كالمن يك فرآيند پنج مرحله‌اي بايستي طي شود شامل:
- مدل‌كردن (Modeling)؛ در مدلسازی باید یک بازه‌زمانی کوچک و تابعی خطی که مسیر گذرا بین حالت‌های متوالی را مشخص می‌کند انتخاب گردد.
- پيش بيني (Forecasting)؛ در این مرحله بردار حالت بعدی به کمک اطلاعات رفتاری سیستم در نمونه قبلی پیش‌بینی می‌گردد.
- تحليل تغيير (Innovation Analysis)؛ اين امكان وجود دارد كه قبل از عمل فيلتركردن، خطاهاي موجود در مجموعه اندازه‌گيري‌ها تشخيص داده شود كه این عمل توسط تحليل تغيير انجام مي‌شود.
- فرآيند فيلتركردن (Filtering)؛ در اين مرحله، به محض اينكه بردار اندازه‌گيري در نمونه زماني بعدی فراهم شود، مي توان بردار حالت سيستم را تخمين زد.
- تحليل باقيمانده (Residual Analysis)؛ بردار باقیمانده به صورت اختلاف بین بردار اندازه‌گیری و بردار فیلتر شده و تخمینی تعریف می‌گردد.
هر پنج مرحله مذكور بايستي در هر تخمين حالت ديناميكي اجرا شود تا بردار حالت تخمين زده شود. رفتار تعداد زیادی از سیستم‌های دینامیک واقعی را نمی‌توان به طور دقیق با فیلتر کالمن مدلسازی کرد. چراکه اکثر سیستم‌های واقعی غیرخطی هستند و فیلتر کالمن ابتدایی با معادلات خطی سروکار دارد. مدل نشدن دینامیک سیستم کارآیی فیلتر را در تخمین حالت شبکه قدرت کاهش می‌دهد. برای حل این مشکل راهکارهای مختلفی پیشنهاد شده است که یکی از آن‌ها استفاده از فیلتر کالمن توسعه یافته (EKF) می‌باشد.
فیلتر کالمن توسعه‌یافته (EKF)
به منظور توصیف الگوریتم فیلتر کالمن گسسته، از تعریف متغیر حالت $x$ به صورت زیر شروع میکنیم:
$$\dot x = \frac{{{\rm{x}}\left( {\rm{k}} \right) - x\left( {k - 1} \right)}}{{\Delta t}}\\
\Rightarrow {\rm{x}}\left( {\rm{k}} \right) = \dot x\Delta t + x\left( {k - 1} \right)\,\,\,(1)$$
که در آن $\Delta t$ گام زمانی بوده و $k$ و $k – 1$ برای نمایش زمان‌های $k\Delta t$ و $\left( {k – 1} \right)\Delta t$ به کار می‌روند. با افزودن معادلات حالت شبکه می‌توان نوشت:
$${\rm{x}}\left( {\rm{k}} \right) = x\left( {k - 1} \right) + \Delta t \times f\left( {x,u,w} \right)\,\,(2)$$
و یا:
$${{\rm{x}}_{\rm{k}}} = \Delta t \times f\left( {x,u,w} \right) + {x_{k - 1}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)$$
با این تعریف می‌توان معادلات سیستم گسسته در زمان را به صورت زیر نوشت:
$$\left\{ \begin{array}{l}
{x_k} = {f_{k - 1}}\left( {{x_{k - 1}},{u_{k - 1}},{w_{k - 1}}} \right)\\
{y_k} = {h_k}\left( {{x_k},{u_k},{v_k}} \right)
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4)$$
برای تغییر این متن بر روی دکمه ویرایش کلیک کنید. لورم ایپسوم متن ساختگی با تولید سادگی نامفهوم از صنعت چاپ و با استفاده از طراحان گرافیک است.
که در آن:
- ${f_k}$: تابع سیستم
- ${x_k}$: بردار حالت سیستم
- ${u_k}$: بردار ورودی سیستم
- ${w_k}$: نویز گوسی مستقل فرآیند با میانگین صفر و کوواریانس${Q_k}$
- ${h_k}$: تابع خروجی
- ${y_k}$: متغیر اندازه‌گیری شده
- ${v_k}$: نویز گوسی مستقل اندازه‌گیری با میانگین صفر و کوواریانس${R_k}$
با در نظرگیری این موارد الگوریتم زمان گسسته فیلتر کالمن توسعه یافته را می‌توان به صورت دو مرحله زیر در نظر گرفت:
- مقدار دهی اولیه فیلتر در $k = 0$:
$$\left\{ \begin{array}{l}
\hat x_0^ + = E\left[ {{x_0}} \right]\\
P_0^ + = E\left[ {\left( {{x_0} - \hat x_0^ + } \right){{\left( {{x_0} - \hat x_0^ + } \right)}^T}} \right]
\end{array} \right.\,\,\,(5)$$
که در آن $E$ نشان دهنده مقدار انتظاری و علامت + نشان‌دهنده تقریب پسین است.
- برای $k = 1,2,…$ باید مراحل زیر اجرا شود:
- محاسبه ماتریس مشتقات جزئی:
$${F_{k - 1}} = {\left. {\frac{{\partial {f_{k - 1}}}}{{\partial x}}} \right|_{\hat x_{k - 1}^ + }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(6)$$
- به روز رسانی زمانی تخمین حالت و کواریانس خطای تخمین:
$$\left\{ \begin{array}{l}
P_k^ - = {F_{k - 1}}P_{k - 1}^ + F_{k - 1}^T + {Q_{k - 1}}\\
\hat x_k^ - = {f_{k - 1}}\left( {\hat x_{k - 1}^ + ,{u_{k - 1}},0} \right)
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(7)$$
- محاسبه ماتریس مشتقات جزئی:
$${H_k} = {\left. {\frac{{\partial {h_k}}}{{\partial x}}} \right|_{\hat x_k^ - }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(8)$$
- به روز رسانی اندازه‌گیری تخمین حالت و کواریانس خطای تخمین:
$$\left\{ \begin{array}{l}
{K_k} = P_k^ - H_k^T{\left( {{H_k}P_k^ - H_k^T + {R_k}} \right)^{ - 1}}\\
\hat x_k^ + = \hat x_k^ - + {K_k}\left( {{y_k} - h\left( {\hat x_k^ - ,0} \right)} \right)\\
P_k^ + = \left( {I - {K_k}{H_k}} \right)P_k^ -
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(9)$$
معایب فیلتر کالمن توسعه یافته
با وجود برتری فیلتر مذکور در پیاده‌سازی فرآیند غیرخطی نسبت به فیلتر کالمن ولی محدودیتها و نقایصی نیز دارد:
بیان سیستم توسط مدل ریاضی یکی از توانایی‌های فیلتر کالمن توسعه یافته است. طراحی فیلتر موردنظر نیازمند اطلاعات کافی از سیستم است تا در نهایت بتوان فرآیند را به وسیله معادلات دیفرانسیل بیان کرد. در عمل بیان دقیق معادلات سیستم سخت‌ترین بخش طراحی فیلتر کالمن است.
مدلسازی دقیق اغتشاش سیستم به عنوان بخش حساس دیگری در طراحی فیلتر کالمن شناخته می‌شود. در حضور توابع غیرخطی حالت سیستم توسط تابعی غیرخطی و حالت پیشین سیستم پیش‌بینی می‌شود. کوواریانس نیز با خطی‌سازی معادلات دینامیک پیش‌بینی می‌شود. خطی سازی همیشه نمی‌تواند کاربردی و مفید باشد. درصورتیکه توابع سیستم به شدت غیرخطی باشند، خطای مدل در پیش‌بینی حالت سیستم و کوواریانس افزایش می‌یابد. در سامانه‌های با این مشخصات، خطی‌سازی و بهره‌گیری از فیلتر کالمن توسعه یافته نمی‌تواند راه حل بهینه باشد و در بعضی مواقع در صورتیکه بازه‌زمانی محاسبات به اندازه کافی کوچک اختیار نشود باعث واگرایی فیلتر می‌گردد. عیب مورد نظر به کمک فیلتر کالمن تأثیرناپذیر قابل حذف است.
در سیستم‌های بزرگ و پیچیده محاسبات ماتریس ژاکوبین به اندازه‌ای پیچیده است که اجرای الگوریتم به صورت زمان واقعی امکان‌پذیر نیست.
حذف جملات مرتبه بالاتر باعث کاهش دقت پیش‌بینی و تخمین می‌گردد.
برای رفع این مشکلات فیلتر کالمن تأثیر ناپذیر (UKF) توضیه شده است. این فیلتر دارای مزیت‌هایی از جمله دقت و سادگی است.
فیلتر کالمن تأثیرناپذیر (UKF)
یک سیستم را با معادلات به فرم $y = g\left( x \right)$ در نظر می‌گیریم. سوال این است که با داشتن تابع چگالی احتمال $x$ چگونه می‌توان میانگین (${\bar y^{UKF}}$) و واریانس ($P_y^{UKF}$) متغیر تصادفی $y$ را محاسبه نمود. تبدیل تأثیر ناپذیر بر این اساس بنا نهاده شده است که:
تقریب یک توزیع احتمال از تقریب یک تابع غیرخطی دلخواه ساده‌تر است.
ایده اصلی این فیلتر در شکل (1) نشان داده شده است. در این شکل مجموعه‌ای از نقاط ${x^{\left( i \right)}}\,\,\left( {i = 1,2,…,2n + 1} \right)$ به نام نقاط سیگما به گونه‌ای انتخاب می‌شوند که میانگین آن‌ها ${\bar y^{UKF}}$ و کواریانس آن‌ها $P_y^{UKF}$ باشد. تابع غیرخطی بر روی هر نقطه اعمال می‌گردد به گونه‌ای که ابری از نقاط تبدیل یافته ایجاد گردد. برآورد خصوصیات آماری نقاط تبدیل یافته تخمینی از میانگین و کواریانس غیرخطی خواهد بود.
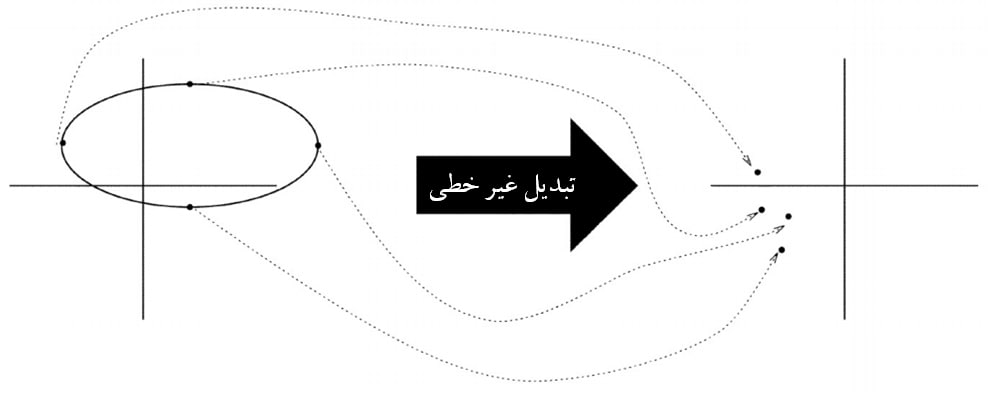
در تبدیل تأثیر ناپذیر هر نقطه سیگما یک وزن ${W^{\left( i \right)}}$ دارد. گام‌های زیر باید برای تعیین میانگین و کواریانس این الگوریتم طی شود:
- هر نقطه سیگما باید از طریق تابع غیر خطی انتشار یابد:
$${y^i} = g\left( {{x^{\left( i \right)}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(10)$$
- میانگین به کمک متوسط وزن‌دار نقاط تبدیل یافته محاسبه می‌شود:
$${\bar y^{UKF}} = \sum\limits_{i = 0}^p {{W^{\left( i \right)}}{y^{\left( i \right)}}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(11)$$
که در آن رابطه زیر بین ضرایب وزنی برقرار است:
$$\sum\limits_{i = 0}^p {{W^{\left( i \right)}} = 1} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(12)$$
- کواریانس را می‌توان از ضرب خارجی نقاط تبدیل یافته محاسبه نمود:
$$P_y^{UKF} = \sum\limits_{i = 0}^p {{W^{\left( i \right)}}\left( {{y^{\left( i \right)}} - \bar y} \right){{\left( {{y^{\left( i \right)}} - \bar y} \right)}^T}} \,\,\,(13)$$
در ادامه الگوریتم فیلتر کالمن توسعه یافته را مدنظر قرار می‌دهیم. برای این منظور سیستم غیرخطی گسسته در زمان با معادلات زیر را در نظر می‌گیریم:
$$\left\{ \begin{array}{l}
{x_{k + 1}} = f\left( {{x_k},{u_k},{t_k}} \right) + {w_k}\\
{y_k} = h\left( {{x_k},{u_k},{t_k}} \right) + {v_k}\\
\left\{ {{w_k}} \right\}\~\left( {0,{Q_k}} \right)\\
\left\{ {{v_k}} \right\}\~\left( {0,{R_k}} \right)
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(14)$$
الگوریتم فیلتر کالمن توسعه یافته را می‌توان به صورت گام‌های زیر در نظر گرفت:
- مقداردهی اولیه در $k = 0$:
$$\left\{ \begin{array}{l}
\hat x_0^ + = E\left[ {{x_0}} \right]\\
P_0^ + = E\left[ {\left( {{x_0} - \hat x_0^ + } \right){{\left( {{x_0} - \hat x_0^ + } \right)}^T}} \right]
\end{array} \right.\,\,\,(15)$$
که در آن $E$ نشان دهنده مقدار انتظاری و علامت + نشان‌دهنده تقریب پسین است.
- معادلات زیر جهت به روز رسانی زمانی مقادیر تخمین حالت و کواریانس از یک مرحله به مرحله دیگر استفاده می‌شوند.
- برای رفتن از زمان $k – 1$ به زمان $k$، نقطه سیگما $x_{k – 1}^{\left( i \right)}$ را با توجه به بهترین حدس‌ها در مورد میانگین و کواریانس $\hat x_{k – 1}^ + $ و $P_{k – 1}^ + $ انتخاب میکنیم:
$$\left\{ \begin{array}{l}
x_{k - 1}^{\left( i \right)} = \hat x_{k - 1}^ + + {{\tilde x}^{\left( i \right)}}\,\,\,\,i = 1,...,2n\\
{{\tilde x}^{\left( i \right)}} = {\left( {\sqrt {nP_{k - 1}^ + } } \right)^T}\,\,\,\,i = 1,...,n\\
{{\tilde x}^{\left( {n + i} \right)}} = - {\left( {\sqrt {nP_{k - 1}^ + } } \right)^T}\,\,\,\,i = 1,...,n
\end{array} \right.\,\,\,(16)$$
- از تابع مشخص غیر خطی $f$ برای تبدیل نقاط سیگما به بردار $\hat x_{k - 1}^{\left( i \right)}$ استفاده میکنیم:
$$\hat x_k^{\left( i \right)} = f\left( {\hat x_{k - 1}^{\left( i \right)},{u_k},{t_k}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(17)$$
- بردارهای $\hat x_{k – 1}^{\left( i \right)}$ را با یکدیگر ترکیب میکنیم تا تخمین حالت پیشین را در زمان $k$ به دست آوریم:
$$x_k^ - = \frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {x_k^{\left( i \right)}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(18)$$
- کواریانس خطای پیشین را به صورت زیر تخمین می‌زنیم:
$$P_k^ - = \\
\frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {\left( {\hat x_k^{\left( i \right)} - \hat x_k^ - } \right){{\left( {\hat x_k^{\left( i \right)} - \hat x_k^ - } \right)}^T}} + {Q_{k - 1}}\,(19)$$
- پس از به روز رسانی زمانی، به روز رسانی اندازه‌گیری به صورت زیر انجام می‌شود:
- نقاط سیگما $\hat x_{k – 1}^ – $ را با توجه به بهترین حدس‌ها در مورد میانگین و کواریانس $\hat x_k^ – $ و $P_k^ – $ انتخاب میکنیم:
$$\left\{ \begin{array}{l}
x_k^{\left( i \right)} = \hat x_k^ - + {{\tilde x}^{\left( i \right)}}\,\,\,\,i = 1,...,2n\\
{{\tilde x}^{\left( i \right)}} = {\left( {\sqrt {nP_k^ - } } \right)^T}\,\,\,\,i = 1,...,n\\
{{\tilde x}^{\left( {n + i} \right)}} = - {\left( {\sqrt {nP_k^ - } } \right)^T}\,\,\,\,i = 1,...,n
\end{array} \right.\,\,(20)$$
- از تابع مشخص غیرخطی $h$ برای تبدیل نقاط سیگما به بردار $\hat y_k^{\left( i \right)}$ استفاده میکنیم:
$$\hat y_k^{\left( i \right)} = f\left( {\hat x_k^{\left( i \right)},{t_k}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(21)$$
- بردارهای $\hat y_k^{\left( i \right)}$ را با یکدیگر ترکیب میکنیم تا تخمین اندازه‌گیری را در زمان $k$ به دست آوریم:
$${y_k} = \frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {y_k^{\left( i \right)}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(22)$$
- کواریانس خطای تخمین اندازه‌گیری را به صورت زیر محاسبه میکنیم:
$$P_k^{} = \frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {\left( {\hat y_k^{\left( i \right)} - {{\hat y}_k}} \right){{\left( {\hat y_k^{\left( i \right)} - {{\hat y}_k}} \right)}^T}} \\
... + {R_k}\,\,\,(23)$$
- کواریانس متقابل بین $\hat x_k^ – $ و ${\hat y_k}$ را به صورت زیر محاسبه میکنیم:
$${P_{xy}} = \frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {\left( {\hat x_k^{\left( i \right)} - \hat x_k^ - } \right)} {\left( {\hat y_k^{\left( i \right)} - {{\hat y}_k}} \right)^T}\,\,(24)$$
- به روز رسانی اندازه‌گیری تخمین حالت را می‌توان به کمک معادلات قیلتر کالمن معمولی به صورت زیر انجام داد:
$$\left\{ \begin{array}{l}
{K_k} = {P_{xy}}P_y^{ - 1}\\
\hat x_k^ + = \hat x_k^ - + {K_k}\left[ {{y_k} - {{\hat y}_k}} \right]\\
P_k^ + = P_k^ - - {K_k}{P_y}K_k^T
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(25)$$
مزیت اصلی فیلتر کالمن تأثیرناپذیری آن است که از مدل دقیق سیستم به جای مدل خطی استفاده می‌گردد. علاوه بر این از ماتریس‌های ژاکوبین $J$ و هسیان $H$ در این روش استفاده نشده و بنابراین سرعت محاسبات افزایش می‌یابد. در عوض در این روش به تعدادی نقطه سیگما نیاز است. با وجود تمام مزایای فیلتر کالمن تأثیر ناپذیر هنوز هم اشکالاتی در این روش وجود دارد:
- به دلیل تعداد کم نقاط سیگما به کمک این فیلتر نمی‌توان تقریب واقعی را در حالت Global داشت.
- این الگوریتم در مورد سیستم‌های با ماتریس کواریانس تکین مانند سیستم‌های قطعی به خوبی کار نمی‌کند.
- فیلتر کالمن تأثیر ناپذیر دارای محدودیت‌های پیاده‌سازی عملی است از جمله اینکه تخمین ماتریس‌های کواریانس نویز به سادگی امکان‌پذیر نیست. در این حالت اگر تخمین مناسبی از ماتریس‌های کواریانس نویز وجود نداشته باشد ممکن است روش تجزیه به عامل‌های چالسکی به دلیل عدم همبستگی داده‌های دریافتی به خوبی کار نکرده و در نتیجه فرآیند تخمین متوقف می‌گردد.
- این الگوریتم فقط قابل اعمال به سیستم‌هایی با نویز سفید و گوسی است.
اعمال فیلترهای کالمن EKF و UKF بر روی شبکه تک ماشینه متصل به شین بی‌نهایت (SMIB)
در این قسمت برای آشنایی بیشتر با نحوه به کارگیری فیلتر کالمن در تخمین حالت شبکه قدرت، یک سیستم تک ماشینه متصل به شین بی‌نهایت را مطابق شکل (2) در نظر می‌گیریم. مدل ژنراتور سنکرون را به صورت کلاسیک و از مرتبه 4 در نظر می‌گیریم که درآن از سیم‌پیچ‌های میراکننده و دینامیک مدار استاتور صرف نظر می‌شود. این تقریب زمانی امکان‌پذیر است که مطالعه دینامیک‌های سریع مدنظر نباشد. اگرچه تأثیر سیم‌پیچ‌های میراکننده در ضریب دمپینگ رتور در نظر گرفته می‌شود.
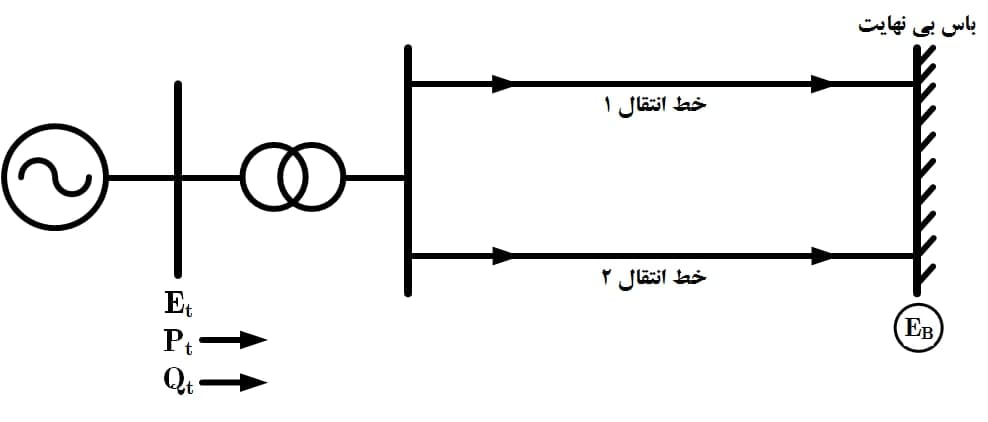
با صرف نظر کردن از مقاومت خط انتقال تمامی توان اکتیو تولید شده توسط ژنراتور به باس بی‌نهایت منتقل می‌شود. همچنین $\delta $ زاویه‌ای است که ${e’_q}$ مولفه محور $q$ ولتاژ پشت راکتانس سنکرون ${x’_d}$ از ولتاژ ترمینال ژنراتور یعنی ${E_t}$ جلوتر است. با در نظرگیری ولتاژ ترمینال به عنوان فازور مرجع می‌توان مدل پریونیتی و غیرخطی مرتبه چهار ژنراتور سنکرون را به صورت زیر نوشت:
$$\left\{ \begin{array}{l}
\dot \delta = {\omega _0}\Delta \omega \\
\Delta \dot \omega = \frac{1}{J}\left( {{T_m} - {T_e} - D\Delta \omega } \right)\\
{{\dot e'}_q} = \frac{1}{{{{T'}_{do}}}}\left( {{E_{fd}} - {{e'}_q} - \left( {{x_d} - {{x'}_d}} \right)\,{i_d}} \right)\\
{{\dot e'}_d} = \frac{1}{{{{T'}_{qo}}}}\left( { - {{e'}_d} - \left( {{x_q} - {{x'}_q}} \right)\,{i_q}} \right)
\end{array} \right.\,\,(26)$$
که در آن ${\omega _0} = 2\pi f$ سرعت نامی سنکرون بر حسب رادیان بر ثانیه و $\omega $ سرعت رتور بر حسب پریونیت است. ${T_m}$ گشتاور مکانیکی ورودی بر حسب پریونیت و ${T_e}$ گشتاور فاصله هوایی یا توان الکتریکی خروجی بر حسب پریونیت هستند. ${E_{fd}}$ ولتاژ خروجی تحریک برحسب پریونیت و $\delta $ زاویه رتور بر حسب رادیان الکتریکی هستند. متغیرهای حالت و ورودی‌های این شبکه را می‌توان به صورت زیر تعریف نمود:
$$\left\{ \begin{array}{l}
x = [\delta \,\,\Delta \omega \,\,{{e'}_q}\,\,{{e'}_d}] = [{x_1}\,\,{x_2}\,\,{x_3}\,\,{x_4}]\\
u = [{T_m}\,\,{E_{fd}}] = [{u_1}\,\,{u_2}]
\end{array} \right.\,(27)$$
بنابراین رابطه (26) را می‌توان به صورت زیر نوشت:
$$\left\{ \begin{array}{l}
{{\dot x}_1} = {\omega _0}{x_2}\\
{{\dot x}_2} = \frac{1}{J}\left( {{u_1} - {T_e} - D{x_2}} \right)\\
{{\dot x}_3} = \frac{1}{{{{T'}_{do}}}}\left( {{u_2} - {x_3} - \left( {{x_d} - {{x'}_d}} \right)\,{i_d}} \right)\\
{{\dot x}_4} = \frac{1}{{{{T'}_{qo}}}}\left( { - {x_4} - \left( {{x_q} - {{x'}_q}} \right)\,{i_q}} \right)
\end{array} \right.\,\,\,\,(28)$$
رابطه میان گشتاور الکتریکی و توان الکتریکی خروجی ژنراتور سنکرون را نیز می‌توان به صورت زیر نوشت:
$${T_e} = {P_t} + {R_a}I_t^2\,\,\,\\
\mathop \to \limits^{{R_a} = 0} \,\,\,\,{T_e} \cong {P_t} = {e_d}{i_d} + {e_q}{i_q}\,\,(29)$$
ولتاژ محورهای $d$ و $q$ را می‌توان به صورت زیر نوشت:
$$\left\{ \begin{array}{l}
{e_d} = {V_t}\sin \delta \\
{e_q} = {V_t}\cos \delta
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(30)$$
و در نتیجه ولتاژ ترمینال ژنراتور برابر خواهد بود با:
$${E_t} = {V_t} = \sqrt {e_d^2 + e_q^2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(31)$$
جریان‌های محور $d$ و $q$ نیز عبارتند از:
$$\left\{ \begin{array}{l}
{i_d} = {I_t}\sin \left( {\delta + \Phi } \right) = \frac{{{{e'}_q} - {V_t}\cos \delta }}{{{{x'}_d}}}\\
{i_q} = {I_t}\cos \left( {\delta + \Phi } \right) = \frac{{{V_t}\sin \delta }}{{{x_q}}}
\end{array} \right.\,\,\,\,\,(32)$$
و جریان ترمینال ژنراتور برابر خواهد بود با:
$${I_t} = \sqrt {i_d^2 + i_q^2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(33)$$
با جایگذاری روابط متغیرهای حالت، جریان‌های محورهای $d$ و $q$ عبارتند از:
$$\left\{ \begin{array}{l}
{i_d} = \frac{{{x_3} - {V_t}\cos {x_1}}}{{{{x'}_d}}}\\
{i_q} = \frac{{{V_t}\sin {x_1}}}{{{x_q}}}
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(34)$$
با جایگذاری (30) و (34) در (29) و ساده‌سازی توان الکتریکی خروجی ژنراتور به صورت زیر خواهد بود:
$${y_1} = {P_t} = \\
\frac{{{V_t}}}{{{{x'}_d}}}{{e'}_q}\sin \delta + \frac{{V_t^2}}{2}\left( {\frac{1}{{{x_q}}} - \frac{1}{{{{x'}_d}}}} \right)\sin 2\delta \,\,\,(35)$$
که در آن ${P_t}$ خروجی قابل اندازه‌گیری سیستم است. در قالب متغیرهای حالت می‌توان نوشت:
$${y_1} = {P_t} = \\
\frac{{{V_t}}}{{{{x'}_d}}}{x_3}\sin {x_1} + \frac{{V_t^2}}{2}\left( {\frac{1}{{{x_q}}} - \frac{1}{{{{x'}_d}}}} \right)\sin 2{x_1}\,\,\,(36)$$
با مطالب مطرح شده تاکنون می‌توان مدل فضای حالت ژنراتور سنکرون را جهت بکارگیری در پروسه تخمین حالت به صورت زیر بیان نمود (بردار ورودی $u$ نیز با توجه به معادلات اخیر به صورت نشان‌داده شده تصحیح می‌گردد):
$$\left\{ \begin{array}{l}
x = [\delta \,\,\Delta \omega \,\,{{e'}_q}\,\,{{e'}_d}] = [{x_1}\,\,{x_2}\,\,{x_3}\,\,{x_4}]\\
u = [{T_m}\,\,{E_{fd}}\,\,{V_t}] = [{u_1}\,\,\,\,{u_2}\,\,{u_3}]\\
{{\dot x}_1} = {\omega _0}{x_2}\\
{{\dot x}_2} = \frac{1}{J}\left( {{T_m} - \left( {\frac{{{V_t}}}{{{{x'}_d}}}{x_3}\sin {x_1} + ...} \right.} \right.\\
...\left. {\left. {\frac{{V_t^2}}{2}\left( {\frac{1}{{{x_q}}} - \frac{1}{{{{x'}_d}}}} \right)\sin 2{x_1}} \right) - D{x_2}} \right)\\
{{\dot x}_3} = \frac{1}{{{{T'}_{do}}}}\left( {{E_{fd}} - {x_3} - \left( {{x_d} - {{x'}_d}} \right) \times ...} \right.\\
...\left( {\frac{{{x_3} - {V_t}\cos {x_1}}}{{{{x'}_d}}}} \right)\left. \, \right)\\
{{\dot x}_4} = \frac{1}{{{{T'}_{qo}}}}\left( { - {x_4} - \left( {{x_q} - {{x'}_q}} \right)\,\frac{{{V_t}\sin {x_1}}}{{{x_q}}}} \right)\\
{y_1} = \frac{{{V_t}}}{{{{x'}_d}}}{x_3}\sin {x_1} + \frac{{V_t^2}}{2}\left( {\frac{1}{{{x_q}}} - \frac{1}{{{{x'}_d}}}} \right)\sin 2{x_1}
\end{array} \right.(37)$$
که در آن همه پارامترها و مقادیر به جز متغیرهای حالت مشخص بوده و قابل اندازه‌گیری هستند. بنابراین می‌توان رابطه (37) را به صورت کلی زیر نمایش داد:
$$\left\{ \begin{array}{l}
\dot x = f\left( {x,u,w} \right)\\
y = h\left( {x,u,v} \right)
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(38)$$
که در آن $x$ نشان دهنده بردار متغیر حالت، $w$ نشان دهنده نویز فرآیند، $v$ نشان دهنده نویز اندازه‌گیری، $f$ تابع سیستم، $h$ تابع خروجی، $u$ سیگنال ورودی و $y$ خروجی قابل اندازه‌گیری است.