تخمین حالت کلاسیک در سيستم‌هاي قدرت
تعداد بازدید: 5374
زمان مطالعه: 6 دقیقه
فهرست مطالب این نوشته
مقدمه
تخمين حالت، عمل تخصيص مقدار به يك متغير حالت نامعلوم سيستم بر طبق معياري به خصوص است كه با استفاده از اندازه گيري از آن سيستم انجام مي شود. معمولاً اندازه گيري، حالات ناقص و اضافي دارد و عمل تخمين حالت سيستم، براساس روش‌هاي آماري صورت مي‌پذيرد كه با حداكثر و يا حداقل كردن معياري به خصوص، مقادير واقعي متغيرهاي حالت تخمين زده مي‌شوند. معيار رايج و آشنا اين است كه مجموع مربعات تفاوت بين مقادير تخميني و حقيقي (يعني اندازه گيري شده) حداقل شود. ايده تخمين حالت براساس حداقل مربعات از اوائل قرن نوزدهم وجود داشته است. پيشرفت عمده در اين زمينه در كاربرد آن در مسائل هوا فضا در قرن بيستم اتفاق افتاده است و در سيستم‌هاي قدرت از اواخر 1960 ميلادي عنوان شد.
اثر عدم تشخيص درست تخمين‌گر حالت در يك سيستم عملي و كاربردي را مي توان در خاموشي آمريكا و كانادا در سال 2003 جستجو كرد. در 14 آگوست 2003 خاموشي گسترده‌اي در بخش‌هايي از آمريكاي شمالي و كاناداي شرقي رخ داد كه بزرگترين خاموشي در تاريخچة آمريكاي شمالي بود كه حدود 50 ميليون نفر تحت تأثير اين خاموشي قرار گرفتند. خاموشي از ساعت 4 بعدازظهر به وقت محلي شروع شد و در بخش‌هايي از آمريكاي شمالي تا 4 روز نيز اين خاموشي ادامه داشت. در گزارش نهايي اين حادثه، چهار عامل براي اين حادثه معرفي شد كه هر يك به نحوي در اين حادثه نقش داشتند كه يكي از عوامل، عدم كارآيي درست تخمين‌گر حالت در حالت بروز خطا و شناسايي آن بود.
تخمين‌گرهاي حالت اساساً فراخور تغييرات بار يا تغييرات ساختار شبكه، به تناوب در سيستم قدرت اجرا مي شوند (به عنوان مثال در هر 5 دقيقه). تخمين‌گر حالت ورودي‌هايي را از سيستم SCADA و هم چنين ساختار شبكه دريافت مي‌كند و حالت‌هاي سيستم را در يك پايگاه داده ذخيره مي‌كند. توجه به اين نكته ضروري است كه قبل از اجراي تخمين‌گر حالت بايستي ساختار شبكه تعيين شود. كاربردهاي ديگر سيستم قدرت نظير تحليل امنيت، پخش بار بهينه، محاسبات اتصال‌كوتاه و … بر پايه نتايج تخمين‌گر حالت اجرا خواهد شد.
تخمین حالت به روش حداقل مربعات وزن‌دار
تخمين حالت در سيستم‌هاي قدرت به عنوان يك مسئله حداقل مربعات وزن‌دار (WLS) توسط Schweppe در مقالات دهه 70 معرفي گرديد. در این روش، تخمین حالت بهترین وضعیت سیستم را با توجه به داده‌های ورودی تعیین می‌کند. این داده‌های ورودی معمولاً عبارتند از:
- مدل شبکه شامل توپولوژی (اتصالات خطوط و وضعیت کلیدهای قدرت) و مشخصات خطوط و ترانس‌ها (امپدانس و نسبت تبدیل ترانس‌ها)
- داده‌های اندازه‌گیری که از طریق سیستم اسکادا تأمین می‌شوند؛ شامل توان حقیقی و راکتیو خطوط، توان تزریقی به باس‌ها، دامنه ولتاژ و جریان.
تخمین‌گر بر اساس این داده‌های ورودی، بردار حالت $x$ را محاسبه می‌کند، که شامل دامنه‌های ولتاژ و زاویه فاز باس‌های شبکه است. عمل تخمین حالت در حالت کلاسیک به کمک تخمین حداقل مربعات وزن‌دار غیر خطی انجام می‌شود. رابطه اندازه‌گیری‌های شبکه با متغیرهای حالت را می‌توان به صورت زیر نمایش داد:
$$z = h\left( x \right) + e\,\,\,\,\,\,\,\,\,\,(1)$$
- $z$: بردار اندازهگیریها
- $h\left( x \right)$: بردار توابع غیرخطی که اندازهگیریها را به بردار حالت $x$ مربوط می‌سازد.
- $e$: بردار خطای اندازه‌گیری.
روش حداقل مربعات وزن‌دار وضعیت شبکه را به گونه‌ای تخمین می‌زند که مجموع مربعات باقی‌مانده‌های اندازه‌گیری که با کواریانس‌های خطا وزن‌دار شده‌اند، مینیمم شوند. به عبارت دیگر برای رسیدن به جواب باید تابع هدف زیر بهینه شود:
$$J\left( x \right) = \sum\limits_{i = 1}^m {\frac{{{{\left( {{z_i} - {h_i}\left( x \right)} \right)}^2}}}{{{R_{ii}}}}} \,\,\,\,\,\,\,\,\,\,(2)$$
که در آن $m$ تعداد کل اندازهگیریها است. رابطه (2) را به فرم ماتریسی نیز می‌توان نوشت:
$$J\left( x \right) = {\left[ {z - h\left( x \right)} \right]^T}{R^{ - 1}}\left[ {z - h\left( x \right)} \right]\,\,\,\,\,\,\,\,\,\,(3)$$
که در آن $R$ ماتریس کواریانس خطاهای اندازه‌گیری است:
$$R = \left[ {\begin{array}{*{20}{c}}
{\sigma _1^2}&{}&{}&{}\\
{}&{\sigma _2^2}&{}&{}\\
{}&{}&{...}&{}\\
{}&{}&{}&{\sigma _m^2}
\end{array}} \right]\,\,\,\,\,\,\,\,\,\,(4)$$
رابطه (3) باید به صورت بازگشتی بهینه شود تا زمانیکه مقدار تفاوت حالت‌ها در دو تکرار از مقدار مشخصی کمتر گردد. با در نظرگیری مقدار اولیه برای حالت سیستم، مقادیر حالت در تکرار $k$ام به صورت زیر تعریف می‌گردد:
$${x^{k + 1}} = {x^k} + \Delta x\,\,\,\,\,\,\,\,\,\,(5)$$
$$\Delta x = {\left( {{H^T}{R^{ - 1}}H} \right)^{ - 1}}{H^T}{R^{ - 1}}\left( {z - h\left( {{x^k}} \right)} \right)\,\,(6)$$
که در آن $H$ ماتریس مشتقات جزئی عناصر $h$ نسبت به مولفه‌های $x$، ماتریس ژاکوبین در تکرار $k$ام است:
$$H = \left[ {\begin{array}{*{20}{c}}
{\frac{{\partial {h_1}\left( x \right)}}{{\partial {x_1}}}}&{\frac{{\partial {h_1}\left( x \right)}}{{\partial {x_2}}}}& \cdots &{\frac{{\partial {h_1}\left( x \right)}}{{\partial {x_n}}}}\\
{\frac{{\partial {h_2}\left( x \right)}}{{\partial {x_1}}}}&{\frac{{\partial {h_2}\left( x \right)}}{{\partial {x_2}}}}& \cdots &{\frac{{\partial {h_2}\left( x \right)}}{{\partial {x_n}}}}\\
\vdots & \vdots & \ddots & \vdots \\
{\frac{{\partial {h_m}\left( x \right)}}{{\partial {x_1}}}}&{\frac{{\partial {h_m}\left( x \right)}}{{\partial {x_2}}}}& \cdots &{\frac{{\partial {h_m}\left( x \right)}}{{\partial {x_n}}}}
\end{array}} \right]\,\,\,\,\,\,\,\,\,\,(7)$$
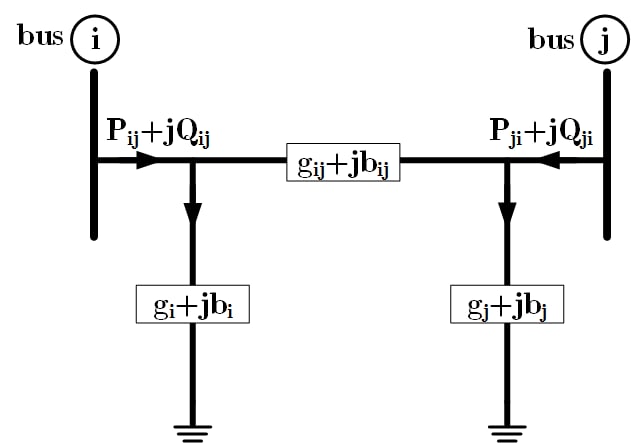
که در آن $n$ تعداد متغیرهای حالت است. مقدار عددی ماتریس $H$ باید در هر تکرار به روز رسانی گردد. برای به دست آوردن عناصر ماتریس $H$، نیاز به محاسبه توابع اندازه‌گیری بر حسب متغیرهای حالت داریم. برای این منظور بخشی از شبکه قدرت را مطابق با شکل (1) شامل دو باس $i$ و $j$ و خط انتقال که با مدل $\pi $ بین این دو باس قرار گرفته است را در نظر می‌گیریم. ${g_{ij}}$ و ${b_{ij}}$ کندوکتانس و سوسپتانس سری خط انتقال و ${g_i}$ و ${b_i}$ سوسپتانس و کندوکتانس موازی خط را نشان می‌دهند.
توابع اندازه‌گیری که اندازه‌گیری‌های اسکادا را به متغیرهای حالت سیستم وابسته می‌سازد در ادامه مورد بررسی قرار می‌گیرد. توان‌های اکتیو و راکتیو تزریقی به باس $i$ را می‌توان به کمک روابط زیر محاسبه نمود:
$${P_i} = {V_i}\sum\limits_{j = 1}^N {{V_j}} \times \\
\left( {{G_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right) + {B_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right)} \right)\,(8)$$
$${Q_i} = {V_i}\sum\limits_{j = 1}^N {{V_j}} \times \\
\left( {{G_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right) - {B_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right)} \right)\,(9)$$
که درآن $N$ تعداد باس‌های متصل به باس $i$ام است. ${G_{ij}}$ و ${B_{ij}}$ نیز به ترتیب قسمت‌های حقیقی و موهومی المان $ij$ام از ماتریس ادمیتانس هستند. از طرفی توان‌های اکتیو و راکتیو عبوری از خط بین باس‌های $i$ و $j$ را می‌توان به صورت روابط زیر نوشت:
$${P_{ij}} = V_i^2\left( {{g_i} + {g_{ij}}} \right) - \\
\,\,{V_i}{V_j}\left( {{g_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right) + {b_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right)} \right)\,(10)$$
$$\,$$
$${Q_{ij}} = - V_i^2\left( {{b_i} + {b_{ij}}} \right) - \\
\,\,{V_i}{V_j}\left( {{g_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right) - {b_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right)} \right)\,(11)$$
دامنه جریان عبوری از خط بین باس $i$ و $j$ نیز برابر است با:
$${I_{ij}} = \frac{{\sqrt {P_{ij}^2 + Q_{ij}^2} }}{{{V_i}}}\,\,\,\,\,\,\,\,\,\,(12)$$
بر پایه این اندازه گیری‌ها ماتریس ژاکوبین $H$ را می‌توان به صورت زیر تشکیل داد:
$$H = \left[ {\begin{array}{*{20}{c}}
{\frac{{\partial {P_{inj}}}}{{\partial \theta }}}&{\frac{{\partial {P_{inj}}}}{{\partial V}}}\\
{\frac{{\partial {P_{flow}}}}{{\partial \theta }}}&{\frac{{\partial {P_{flow}}}}{{\partial V}}}\\
{\frac{{\partial {Q_{inj}}}}{{\partial \theta }}}&{\frac{{\partial {Q_{inj}}}}{{\partial V}}}\\
{\frac{{\partial {Q_{flow}}}}{{\partial \theta }}}&{\frac{{\partial {Q_{flow}}}}{{\partial V}}}\\
{\frac{{\partial {I_{ij}}}}{{\partial \theta }}}&{\frac{{\partial {I_{ij}}}}{{\partial \theta }}}\\
0&{\frac{{\partial {V_i}}}{{\partial V}}}
\end{array}} \right]\,\,\,\,\,\,\,\,\,\,(13)$$
مشتقات جزئی معادلات اندازه‌گیری (8) تا (12) در ادامه بررسی شده است. عناصر مربوط به اندازه‌گیری‌های توان اکتیو تزریقی را می‌توان به صورت روابط زیر نوشت:
$$\frac{{\partial {P_i}}}{{\partial {\theta _i}}} = \\
\sum\limits_{j = 1}^N {{V_i}{V_j}\left( { - {G_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right) + {B_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right)} \right)} \\
- V_i^2{B_{ii}}\,\,(14)$$
$$\,$$
$$\frac{{\partial {P_i}}}{{\partial {\theta _j}}} = \\
{V_i}{V_j}\left( {{G_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right) - {B_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right)} \right)\,(15)$$
$$\,$$
$$\frac{{\partial {P_i}}}{{\partial {V_i}}} = \\
\sum\limits_{j = 1}^N {{V_j}\left( {{G_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right) + {B_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right)} \right)} \\
- {V_i}{G_{ii}}\,(16)$$
$$\,$$
$$\frac{{\partial {P_i}}}{{\partial {V_j}}} = \\
{V_j}\left( {{G_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right) + {B_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right)} \right)\,(17)$$